Travail et énergie cinétique.
Introduction :
I. Energie cinétique d'un solide
1. L’énergie cinétique d’un solide en mouvement de translation
Un système en mouvement possède de l’énergie. L’énergie due à la vitesse est appelée : énergie cinétique : Ec.
L’énergie cinétique dépend de la vitesse et de la masse du solide.
Pour un solide animé d’un mouvement de translation, tous les points du solide ont à chaque instant la même vitesse que le centre d’inertie $\mathbf{G}$ :
L’énergie cinétique $E_C$ d’un solide en mouvement de translation est donnée par la relation
![]()
$$
\mathrm{V} \text { : vitesse de solide ; } \mathrm{m} \text { : masse de solide }
$$
1. L’énergie cinétique d’un solide en mouvement de rotation
Un corps rigide quelconque tourne autour d’un axe de rotation dont la position et l’orientation restent fixe Le corps est constitué de particules ponctuelles de masse $m_i$ situées à une distance $r_i$ de l’axe de rotation.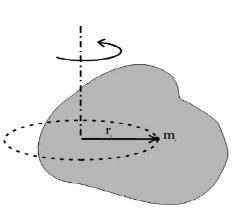 L’énergie cinétique d’une de ces particules est : $\mathrm{Ec}_{\mathrm{i}}=\frac{1}{2} \cdot m_i, v_i^2$
avec $v_i=r_i . \omega ; \omega$ la vitesse angulaire
L’énergie cinétique d’une de ces particules est : $\mathrm{Ec}_{\mathrm{i}}=\frac{1}{2} \cdot m_i, v_i^2$
avec $v_i=r_i . \omega ; \omega$ la vitesse angulaire
$$ \mathrm{Ec}_{\mathrm{i}}=\frac{1}{2} \cdot m_i \cdot r_i^2 \cdot \omega^2 $$
L’énergie cinétique totale de rotation est :
$$ E_C=\sum E_{C_i}=\frac{1}{2} \cdot m_i \cdot r_i^2 \cdot \omega^2=\frac{1}{2} \cdot \omega^2 \cdot \sum m_i \cdot r_i^2 $$
L’énergie cinétique d’un solide en mouvement de rotation peut s’écrire sous la forme:
$$ \operatorname{avec} J_{\Delta}=\sum m_i \cdot r_i^2 $$
$$ \text { La grandeur } J_{\Delta} \text { est appelée le moment d’inertie du corps par rapport à l’axe de rotation ( } \Delta \text { ). } $$
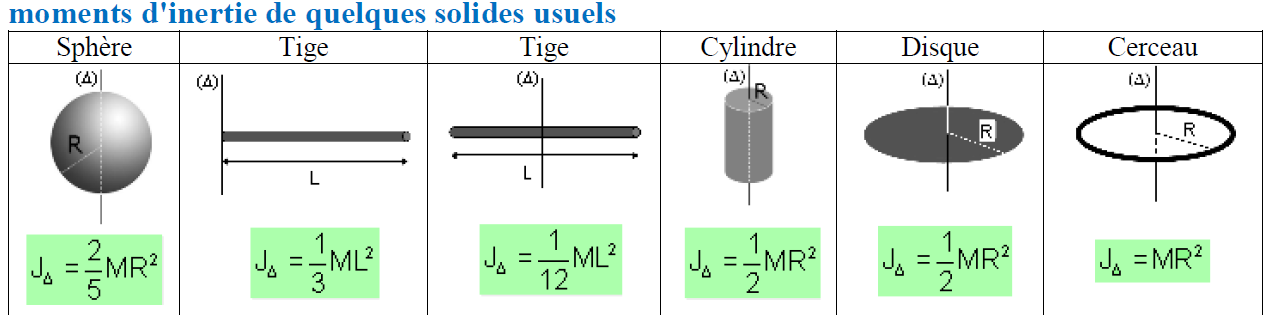
moments d’inertie de quelques solides usuels
| Sphère | Tige | Tige | Cylindre | Disque | Cerceau |
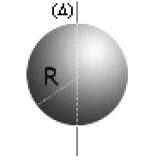 $J_{\Delta}=\frac{2}{5} M^2$
$J_{\Delta}=\frac{2}{5} M^2$ |
 $J_{\Delta}=\frac{1}{3} M L^2$
$J_{\Delta}=\frac{1}{3} M L^2$ |
 $J_{\Delta}=\frac{1}{12} \mathrm{ML}^2$
$J_{\Delta}=\frac{1}{12} \mathrm{ML}^2$ |
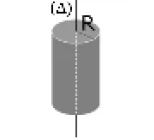 $J_{\Delta}=\frac{1}{2} M R^2$
$J_{\Delta}=\frac{1}{2} M R^2$ |
 $J_{\Delta}=\frac{1}{2} M R^2$
$J_{\Delta}=\frac{1}{2} M R^2$ |
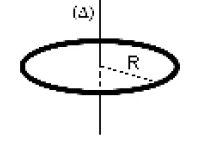 $J_{\Delta}=M R^2$ $J_{\Delta}=M R^2$ |
II. Théorème de l'énergie cinétique
Dans un référentiel galiléen, la variation de l’énergie cinétique $\triangle \mathrm{Ec}$ d’un solide (en translation ou de rotation ) d’un point A à un point $B$ est égale à la somme des travaux des forces qui lui sont appliquées.
$\Delta \mathrm{Ec}=\mathrm{Ec}(\mathrm{B})-\mathrm{Ec}(\mathrm{A})=\Sigma W_{A B}(\vec{F})$
La variation d’énergie cinétique (final – initial) = la somme des travaux de toutes les forces extérieure
Remarque:
- C’est le travail des forces extérieures appliquées qui fait varier l’énergie cinétique du solide : on dit que le travail mécanique est un mode de transfert de l’énergie.
– si le travail des forces appliquées est moteur $\left(\Sigma \mathrm{W}_{\mathrm{AB}}(\vec{F})>0\right)$ l’énergie cinétique du solide augmente donc sa vitesse augmente.
– si le travail des forces appliquées est résistant $\left(\sum W_{A B}(\vec{F})<0\right)$ l’énergie cinétique du solide diminue donc sa vitesse diminue.
- C’est le travail des forces extérieures appliquées qui fait varier l’énergie cinétique du solide : on dit que le travail mécanique est un mode de transfert de l’énergie.