Mouvement de rotation d’un solide non déformable autour d’un axe fixe.
Introduction 1:
Dans notre quotidien, des objets comme les roues, les aiguilles d’une horloge ou les portes illustrent le mouvement de rotation autour d’un axe fixe.
Cette leçon porte sur l’étude du mouvement d’un solide non déformable, c’est-à-dire un objet dont la forme reste invariable. Nous découvrirons :
– L’axe de rotation, qui définit les trajectoires circulaires des points du solide ;
– Les grandeurs associées : angle de rotation, vitesse angulaire, et accélération angulaire ;
– Les principes reliant forces, moments et mouvement.
I. Définition du mouvement de rotation autour d’un axe fixe.
1. Définition
Un solide indéformable possède un mouvement de rotation autour d’un axe fixe si le mouvement de chacun de ses points est circulaire centré sur l’axe de rotation.
Exemple:
Mouvement de la grande roue par rapport à son axe de rotation représentée ci-contre.

2. Remarques sur mouvement de rotation d’un solide indéformable
– Un solide indéformable est un système de points matériels tel que la distance entre deux points quelconques du système est une constante du temps
– Les points du solide situés sur l’axe de rotation, s’ils existent, sont immobiles.
La trajectoire de chaque point de solide appartient au plan perpendiculaire à l’axe de rotation.
II. Repérage d'un point M d’un solide en rotation par rapport à l’axe fixe
1. Abscisse curviligne
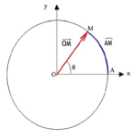
Soit M un point quelconque d’un solide en rotation par rapport à $(\Delta)$. On oriente la trajectoir selon le sens du mouvement. On y choisit un point de référence $M_0$.
La position du point mobile $M$, est repérée par son abscisse curviligne: $\quad s(t)=\widehat{M_0 M}$
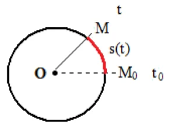
Unité de l’abscisse curviligne est le mètre (m)
2 – Abscisse angulaire
On peut aussi repérer la position du mobile par l’abscisse angulaire $\theta$ qui mesure l’angle de la rotation depuis l’origine $M_0$ sur le cercle donc
$$
\theta(\mathrm{t})=\left(O M_0 ; O M\right)
$$
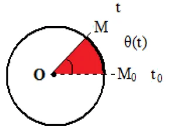
Unité de l’abscisse angulaire est le radian (rad)
3. Relation entre abscisse curviligne et abscisse angulaire
Il existe une relation géométrique simple entre abscisse curviligne et abscisse angulaire :
$$
s(t)=R \cdot \theta(t)
$$
Tel que $\mathbf{R}$ le rayon de la trajectoire circulaire.
III. Vitesse d’un solide en rotation autour d’un axe fixe.
Pour décrire le mouvement de rotation d’un solide indéformable, il suffit d’étudier le mouvement de l’un de ses points n’appartenant pas à l’axe de rotation.
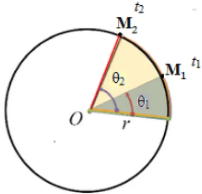
Soit $M$ un point du solide en un mouvement de rotation autours de l’axe ( $\Delta$ )
– à l’instant $\mathrm{t}_1$ la position du point M est noté $\mathrm{M}_1$
– à l’instant t , la position du point M est $\mathrm{M}_2$
1. Vitesse angulaire
1.1. Vitesse angulaire moyenne
Au cours de la durée $\Delta \mathrm{t}=\mathrm{t}_2-\mathrm{t}_1$ le point M parcourt l’arc $\widehat{M_1 M_2}$ en décrivant l’angle $\Delta \theta=\theta_2-\theta_1$ (angle de rotation du solide).
On appelle vitesse angulaire moyenne $\omega_m$, le quotient de l’angle $\Delta \theta$ par l’intervalle de temps $t_2-t_1$ mis pour effectuer cette rotation.
$$
\omega_{\mathrm{m}}=\frac{\theta_2-\theta_1}{\mathrm{t}_2-\mathrm{t}_1}=\frac{\Delta \theta}{\Delta \mathrm{t}}
$$
l’unité de la vitesse angulaire dans SI : rad/s
1.2. Vitesse angulaire instantané
La vitesse angulaire instantanée d’un solide à la date t , se définit comme la vitesse angulaire moyenne du solide pendant une brève durée autour de la date $t$.
$$
\omega(\mathrm{t})=\frac{\theta_2-\theta_1}{\mathrm{t}_2-\mathrm{t}_1}=\frac{\delta \theta}{\delta \mathrm{t}}
$$
Oủ $\delta$ indique une variation infinitésimale ou élémentaire.
(pratiquement en encadrent l’instant $t$ entre deux instants $\mathrm{t}_{\mathrm{i}-1}$ et $\mathrm{t}_{\mathrm{i}+1}$ très proches)
Remarque
La vitesse angulaire $\omega$ est la même pour tous les points du solide indéformable en rotation autours d’un axe fixe. Elle est donc la vitesse angulaire du solide en rotation.
2. Vitesse linéaire
La vitesse linéaire (vitesse tangentielle) du point M à l’instant $t$ est le quotient de la longueur de l’arc $\widehat{M_1 M_2}$ parcouru par la durée $\Delta$ t mise pour le faire :
$\mathrm{v}(\mathrm{t})=\frac{\mathrm{s}_2-\mathrm{s}_1}{\mathrm{t}_2-\mathrm{t}_1}=\frac{\widehat{M_1 M_2}}{\mathrm{t}_2-\mathrm{t}_1} \quad, \quad \widehat{M_1 M_2}=\mathrm{s}_2-\mathrm{s}_1=\Delta \mathrm{s}$
Remarque :
Si $\Delta t$ est grand, on a les vitesses moyennes, si $\Delta t$ est petit on a les vitesses instantanées.
3. Relation entre vitesse angulaire et vitesse d’un point de solide
Pour un point M d’un solide en rotation autour d’un axe fixe, situé à une distance R de l’axe de rotation, la distance parcourue pendant une durée $\Delta \mathrm{t}=\mathrm{t}_2-\mathrm{t}_1$ est :
$\widehat{M_1 M_2}=\mathrm{s}_2-\mathrm{s}_1=\Delta \mathrm{s}$.
De plus, $\Delta \mathrm{s}=\mathrm{s}_2-\mathrm{s}_1=$ R. $\theta_2-$ R. $\theta_2=\mathrm{R} \cdot \Delta \theta$
Donc $\mathrm{v}=\frac{\widehat{M_1 M_2}}{t_2-t_1}=\frac{\mathrm{R} \cdot \Delta \theta}{t_2-t_1}=\mathrm{R} \cdot \frac{\Delta \theta}{\Delta t}$
et comme $\omega=\frac{\Delta \theta}{\Delta \mathrm{t}}$ alors $\quad \mathbf{v}=\mathbf{R} \cdot \omega$
IV. Mouvement de rotation uniforme d’un solide autour d’un axe fixe.
1. Définition d’un mouvement de rotation uniforme
Un solide indéformable est en mouvement de rotation uniforme si sa vitesse angulaire $\omega$ est constante.
On remarque que les points mobiles d’un tel solide sont animés d’un mouvement circulaire uniforme.
2. Equation horaire d’un mouvement circulaire uniforme
Considérons un point M ayant un mouvement circulaire uniforme de centre O , de rayon R et de vitesse linéaire v . Le point M a une vitesse angulaire $\omega$ constante, on peut donc en déduire l’expression de l’angle $\theta(\mathrm{t})$ formé par le vecteur $\overrightarrow{O M}$ et l’axe $(\mathrm{Ox})$ en fonction du temps : c’est l’équation horaire.
3. Les propriétés d’un mouvement circulaire uniforme
Si le mouvement de rotation est uniforme ( $\omega$ est constante), le mouvement est périodique car la durée mise pour effectuer un tour est constante.
3.1. La période
La période T d’un mouvement de rotation uniforme est égale à la durée d’un tour.
Pour un tour on a $\Delta \theta=2 \pi$ rad, alors $\Delta \mathrm{t}=\mathrm{T}$ donc $\omega=\frac{2 \pi}{\mathrm{~T}}$
et alors $\mathrm{T}=\frac{2 \pi}{\omega}$ avec T en ( s ) et $\omega$ en (rad. $\mathrm{s}^{-1}$ ).
3.2. La fréquence
La fréquence $f$ d’un mouvement de rotation uniforme est le nombre des périodes par seconde, donc le nombre des tours par seconde.
$f=\frac{1}{\mathrm{~T}}=\frac{\omega}{2 \pi}$
ce qui donne également $\omega=2 \pi f$ avec $f$ en hertz $(\mathrm{Hz})$.
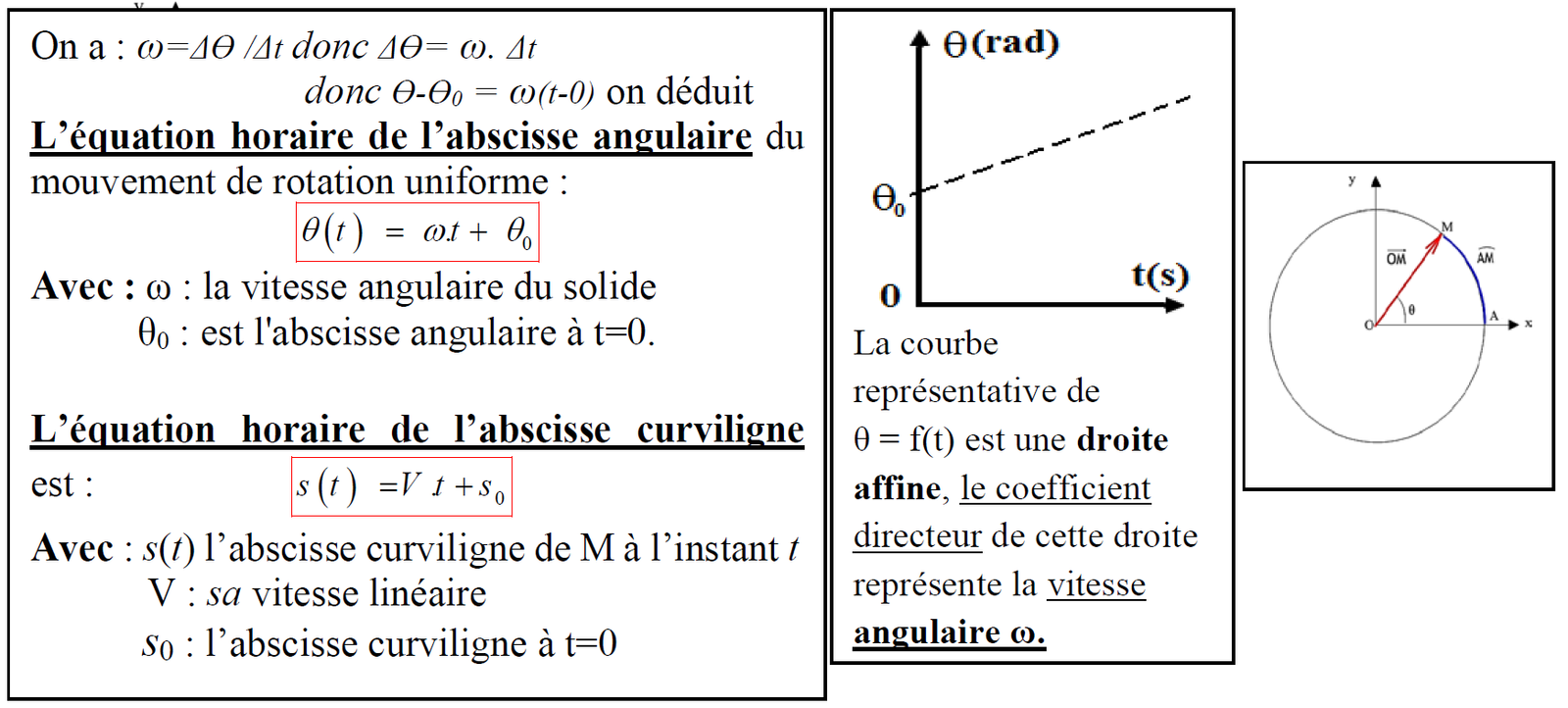
On a : $\omega=\Delta \theta / \Delta t$ donc $\Delta \theta=\omega . \Delta t$
donc $\theta-\theta_0=\omega(t-0)$
On déduit l’équation horaire de l’abscisse angulaire du mouvement de rotation uniforme :
$$
\theta(t)=\omega t+\theta_0
$$
Avec : $\omega$ : la vitesse angulaire du solide $\theta_0$ : est l’abscisse angulaire à $\mathrm{t}=0$.
L’équation horaire de l’abscisse curviligne est:
$$
s(t)=V t+s_0
$$
Avec : $s(t)$ l’abscisse curviligne de Mà l’instant $t$
V : sa vitesse linéaire
$S_0$ : l’abscisse curviligne à $\mathrm{t}=0$
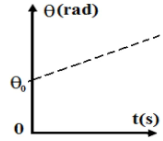
La courbe représentative de $\theta=f(t)$ est une droite affine, le coefficient directeur de cette droite représente la vitesse angulaire $\omega$.