MESURE DES QUANTITES DE MATIERE EN SOLUTION PAR CONDUCTIMETRIE.
Introduction :
I. Conductance d'une solution électrolytique.
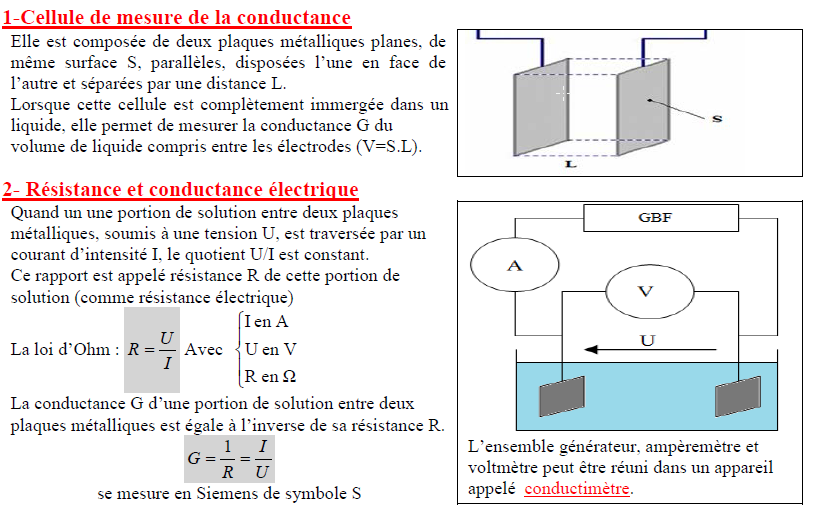
1-Cellule de mesure de la conductance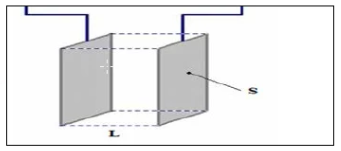
Elle est composée de deux plaques métalliques planes, de même suface S, paralleles, disposées l’une en face de l’autre et séparees par une distance L .
Lorsque cette cellule est complètement immergée dans un liquide, elle permet de mesurer la conductance G du volume de liquide compris entre les électrodes ( $\mathrm{V}=\mathrm{S} . \mathrm{L}$ ).
2-Résistance et conductance électrique
Quand un une portion de solution entre deux plaques métalliques, soumis à une tension U, est traversée par un courant d’intensité I, le quotient $\mathrm{U} / \mathrm{I}$ est constant.
Ce rapport est appelé résistance R de cette portion de solution (comme résistance électrique)
La loi d’Ohm : $R=\frac{U}{I}$ Avec $\left\{\begin{array}{l}\mathrm{Ien} \mathrm{A} \\ \mathrm{U} \text { en V } \\ \mathrm{Ren} \Omega\end{array}\right.$
La conductance G d’une portion de solution entre deux plaques métalliques est égale a l’inverse de sa résistance $R$.
$$
G=\frac{1}{R}=\frac{I}{U}
$$
se mesure en Siemens de symbole S
II. Facteurs influençant la conductance
La conductance $G$ dépend de la nature de la solution.
Pour une solution donnée, la conductance augmente quand:
– La surface S d’une électrode augmente ;
– la distance L entre les électrodes diminue :
– la température $\theta$ de la solution augmente :
– la concentration C de la solution augmente (G est proportionnelle a C ).
III. Courbe d’étalonnage
On réalise une série de mesures de conductance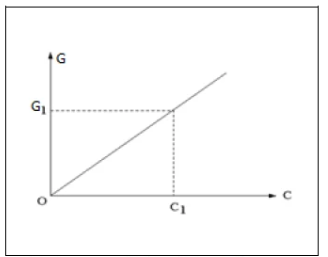
pour des solutions de concentrations connues afin de tracer la courbe d’évolution de cette conductance en fonction de la concentration.
La conductance varie en fonction de la concentration suivant la loi de Kohlrausch: $\quad \mathrm{G}=\mathrm{k} \times \mathrm{C}$
Pour des solutions peu concentrées ( $\mathrm{C}<10^{-2} \mathrm{molL}^{-1}$ ), on constate que la conductance G d’une solution est done proportionnelle à sa concentration C .
Cette courbe détalonnage permet ensuite de retrouver la concentration inconnue de la solution à doser à partir de la mesure de la conductance
Remarque : La méthode d’étalonnage conductimétrique a ses limites, en l’occurrence elle n’est pas applicable lorsque la solution est un mélange de plusieurs espèses ioniques (par exemple de l’eau de mer qui contient différents ions en solution).
IV. La conductivité
1-Définition de la conductivité
La conductivité o représente l’aptitude d’une solution à conduire le courant électrique. Elle est done caractéristique de la solution (elle ne dépend que de la solution et pas des électrodes de mesure).
La conductance d’une solution est proportionnelle au rapport $\mathrm{S} / \mathrm{L}$; on écrit : $\mathrm{G}=\sigma, \frac{S}{L}$ avec
– $\sigma$ est la conductivité de la solution en $\mathrm{S} . \mathrm{m}^{-1}$;
– S est la surface des électrodes en $\mathrm{m}^2$;
– L est la distance entre les plaques en m.
$\frac{S}{L}$ est appelée constante de cellule en $m$.
2-Facteurs influencant la conductivité
La conductivité augmente quand :
– la concentration de la solution augmente ;
– la température de la solution angmente.
Elle dépend aussi de la nature des ions présents dans la solution.
3-Conductivité molaire ionigue d’un ion
La conductivité d’un ion $\mathrm{X}_i$ est proportionnelle à sa concentration pour des valeurs inférieures à $10^{-2} \mathrm{~mol} / \mathrm{L}$.
$$
\sigma_i=\lambda i \cdot[X i]
$$
Le coefficient de proportionnalité $\lambda_{\text {i }}$ est appelé conductivité molaire ionique son unité est le $\mathrm{S} . \mathrm{m}^2 \cdot \mathrm{~mol}^{-1}$.
La conductivité molaire ionique dépend de la température, de la nature du solvant et de l’ion considéré.
4-Conductivité d’une solution
La conductivité $\sigma$ d’une solution depend des ions en solution.
La conductivité $\sigma$ de la solution est égale à la somme des conductivités due aux cations et aux anions. On écrit : $\sigma=\sigma(+)+\sigma(-)$
$$
\sigma=\sum_i \lambda i \cdot\left[X_i\right]=\lambda_1 \cdot\left[\mathrm{X}_1\right]+\lambda_2 \cdot\left[\mathrm{X}_2\right]+\lambda_2\left[\mathrm{X}_3\right]+\ldots . .+\lambda_p\left[\mathrm{X}_{\mathrm{P}}\right]
$$
Avec $\sigma$ en S.m. $\mathrm{m}^{-1} ; \quad \lambda_i$ en S.m² $\mathrm{mol}^{-1}$ et $\left[\mathrm{X}_{\mathrm{i}}\right]$ en mol. $\mathrm{m}^{-3}$ (attention à l’unité !)
Exemple
Pour une solution de concentration C du type $\left(\mathrm{M}^{+} \mathrm{qq}^{+} \mathrm{X}_{\mathrm{qq}}^{-}\right): \quad \sigma=\lambda_{M+} \cdot\left[M^{+}\right]+\lambda_{x–}\left[X^{-}\right]$Or : $\quad\left[\mathrm{M}^{+}{ }_{\text {aq }}\right]=\left[\mathrm{X}_{\text {aq }}^{-}\right]=\mathrm{C}$
Donc: $\quad \sigma=\left(\lambda_{M+}+\lambda_{X-}\right) . C$
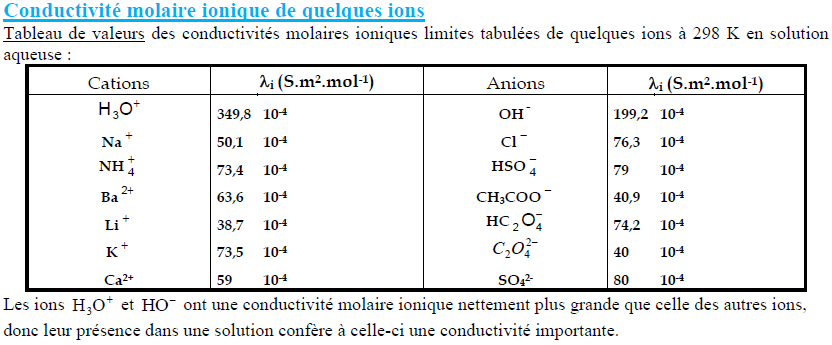
Conductivité molaire ionique de quelques ions
Tableau de valeurs des conductivités molaires ioniques limites tabulées de quelques ions à 298 K en solution aqueuse:
| Cations | $\lambda_{\mathrm{i}}\left(\mathrm{S} . \mathrm{m}^2 \cdot \mathrm{~mol}^{-1}\right)$ | Anions | $\lambda_{\mathrm{i}}\left(\mathrm{S} . \mathrm{m}^2 \cdot \mathrm{~mol}^{-1}\right)$ |
| $\begin{gathered}\mathrm{H}_3 \mathrm{O}^{+} \\ \mathrm{Na}^{+} \\ \mathrm{NH}_4^{+} \\ \mathrm{Ba}^{2+} \\ \mathrm{Li}^{+} \\ \mathrm{K}^{+} \\ \mathrm{Ca}^{2+}\end{gathered}$ | $\begin{array}{ll}349,8 & 10^{-4} \\ 50,1 & 10^{-4} \\ 73,4 & 10^{-4} \\ 63,6 & 10^{-4} \\ 38,7 & 10^{-4} \\ 73,5 & 10^{-4} \\ 59 & 10^{-4}\end{array}$ | $\begin{gathered}\mathrm{OH}^{-} \\ \mathrm{Cl}^{-} \\ \mathrm{HSO}_4^{-} \\ \mathrm{CH}_3 \mathrm{COO}^{-} \\ \mathrm{HC}_2 \mathrm{O}_4^{-} \\ \mathrm{C}_2 \mathrm{O}_4^{2-} \\ \mathrm{SO}_4^{2-}\end{gathered}$ | $$ \begin{array}{ll} 199,2 & 10^{-4} \\ 76,3 & 10^{-4} \\ 79 & 10^{-4} \\ 40,9 & 10^{-4} \\ 74,2 & 10^{-4} \\ 40 & 10^{-4} \\ 80 & 10^{-4} \end{array} $$ |
Les ions $\mathrm{H}_3 \mathrm{O}^{+}$et $\mathrm{HO}^{-}$ont une conductivité molaire ionique nettement plus grande que celle des autres ions, donc leur présence dans une solution confère à celle-ci une conductivité importante.
