LES SOLUTIONS ELECTROLYTIQUES ET LES CONCENTRATIONS.
Introduction :
1. Le solide ionique
Un solide ionique est un solide
composé d’ions. Etant donné qu’un tel solide est toujours électriquement neutre il associe toujours des cations et des anions dont les charges se compensent.
Exemple :
– La formule NaCl indique que le chlorure de sodium comporte autant d’ions sodium que d’ions chlorure. En effet chaque ion ne porte qu’une charge, une charge positive pour $\mathrm{Na}^{+}$et une négative pour $\mathrm{Cl}^{-}$.
2. La molécule polaire
Une molécule est un ensemble d’atomes (au moins deux) identiques ou non, unis les uns aux autres par le biais de liaisons chimiques.
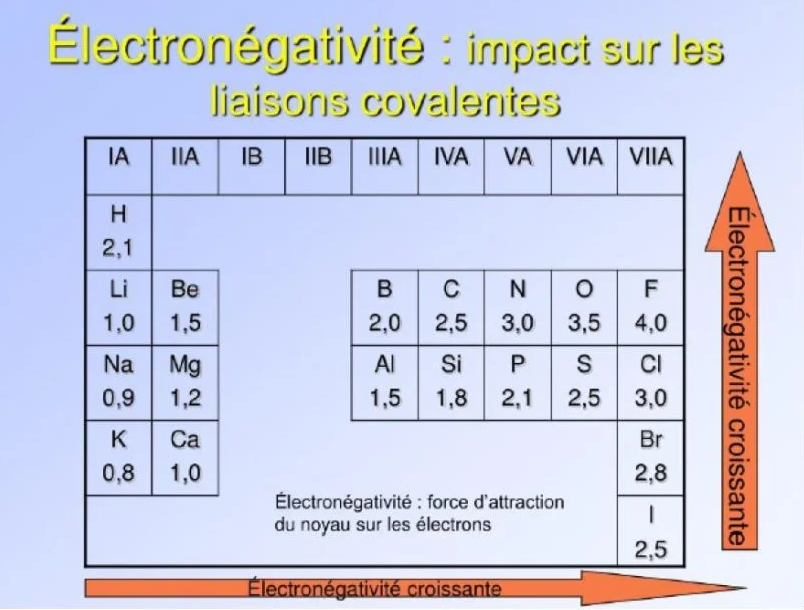
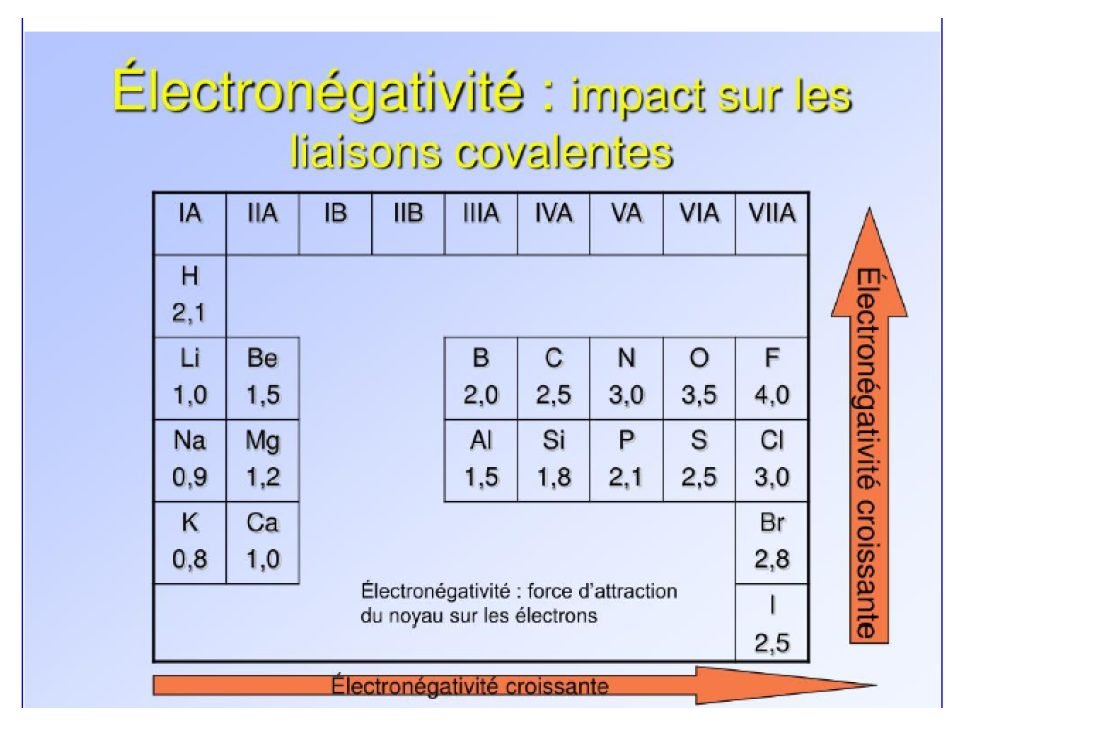
La liaison est dite covalente lorsque deux atomes mettent en commun un électron de leur couche externe. Dans une liaison, le doublet électronique peut ne pas être partagé équitablement entre les deux atomes : l’un des deux atomes peut avoir une force d’attraction sur ce doublet plus grande que l’autre.
On appelle électronégativité cette capacité pour les atomes à attirer le doublet. Ce partage inéquitable de la charge électronique transforme alors le couple atomique en dipôle.
lorsque la différence d’électronégativité est nulle, les charges
partielles sont nulles $(\delta=0)$ et la liaison est complètement apolaire : le doublet électronique est réparti équitablement entre les atomes.
Si deux atomes impliqués dans une liaison de covalence sont d’électronégativités différentes, la répartition des charges est dissymétrique : les électrons de la liaison sont délocalisés vers l’atome le plus électronégatif, qui porte alors une charge partielle négative notée $\boldsymbol{\delta}$. L’autre atome de la liaison porte, quant à lui, une charge partielle positive notée $\delta^{+}$.
Plus les charges sont réparties de façon asymétrique, plus une liaison ou molécule sera polaire la liaison perd alors de son caractère covalent pour tendre vers une liaison ionique pur. la liaison est dite polarisée.
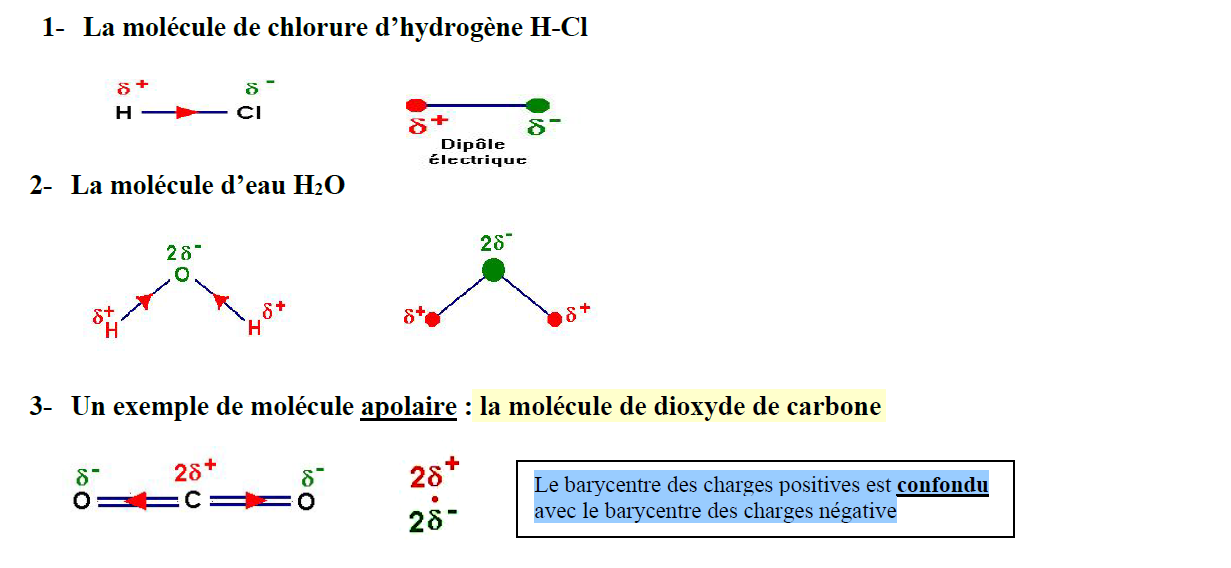
1- La molécule de chlorure d’hydrogène $\mathbf{H – C l}$
$$
2- La molécule d’eau $\mathrm{H}_2 \mathrm{O}$
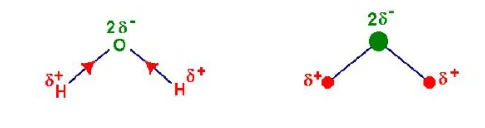
3- Un exemple de molécule apolaire : la molécule de dioxyde de carbone
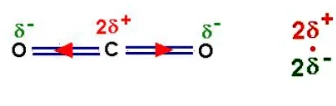
Le barycentre des charges positives est confondu
avec le barycentre des charges négative
3. Les solutions aqueuses électrolytiques
1.Definition d’une solution aqueuse électrolvtique
Une solution électrolytique est obtenue en dissolvant une substance appelée soluté dans un liquide appelé solvant. Le soluté peut être un solide, un liquide ou un gaz. Si le solvant est l’eau la solution obtenue est appelée solution aqueuse.
Une solution électrolytique est une solution contenant des ions. Elle conduit le courant et elle est électriquement neutre.
Remarque: un solvant polaire ne peut dissocier que les molécules polaires et les solides ioniques.
Exemples :
Une solution de chlorure de sodium est notée : $\mathrm{Na}^{+}{ }_{(\mathrm{aq})}+\mathbf{C l}_{(\mathrm{aq})}$ elle est obtenue en dissolvant du chlorure de sodium solide NaCl dans l’eau.
Une solution de chlorure de chlorure d’hydrogène $\mathbf{H}^{+}{ }_{(a q)}+\mathbf{C l}_{(a q)}$ elle est obtenue en dissolvant du chlorure d’hydrogène $\mathbf{H C l}$ gazeux dans l’eau. (Expérience du jet d’eau).
2.Etapes de la dissolution
La dissolution d’un composé ionique comprend trois étapes
| Une dissociation : Les forces électrostatiques qui s’exercent entre le solvant et les ions à la surface du cristal compensent les forces électrostatiques attractives internes du cristal sur ces ions : les ions se détachent du cristal. |  |
| Une solvatation : Les ions dissociés s’entourent de molécules de solvant attirées sous l’effet des forces électrostatiques. Les ions sont solvates. Si le solvant est de l’eau, on ajoute l’indice (aq) en indice à la formule de l’ion. |  |
| Une dispersion : Sous l’effet de l’agitation thermique (ou par une agitation mécanique réalisée par un agent extérieur), les ions solvates se répartissent progressivement dans l’ensemble du solvant. On obtient un mélange homogène : la solution. |  |
3. Équation chimique de la dissolution
La dissolution d’un électrolyte est une transformation chimique, on peut donc lui associer une équation chimique modélisant cette réaction en générale.
$$
\underset{\text { anu }}{\mathbf{A B}} \mathbf{A}_{(\mathrm{aq})}^{+}+\mathbf{B}_{(a q)}^{-}
$$
électrolyte
Exemples
$\mathrm{HCl}_{(\mathfrak{g})} \rightarrow \mathrm{H}_{(\mathrm{aq})}^{+}+\mathrm{Cl}_{(\mathrm{aq})}^{-} \quad, \quad \mathrm{NaCl}_{(\mathrm{s})} \rightarrow \mathrm{Na}_{(\mathrm{aq})}^{+}+\mathrm{Cl}_{(\mathrm{aq})}$
Remarques: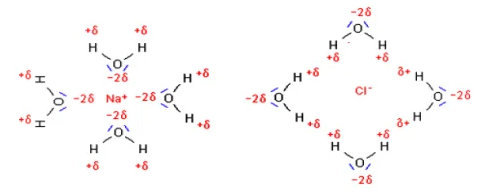
Lors de l’étape de l’hydratation en solution aqueuse, les ions s’entourent de molécules d’eau. Pour indiquer qu’ils sont hydratés, on ajoute l’indice $(\mathrm{aq})$ à leurs symboles.
4. Les concentrations molaires
1. Concentration du soluté apporté ou concentration de la solution.
C’est la quantité de matière de soluté apporté divisée par le volume de la solution obtenue
$$
\boldsymbol{C}=\frac{\boldsymbol{n}_{\text {soluté }}}{\boldsymbol{V}_{\text {solution }}}, \text { avec Cen mol/L, n(soluté) en mol et } \mathrm{V} \text { (solution) en } \mathrm{L}
$$
2. Concentration effective des espèces présentes dans la solution
On emploie une notation différente pour la concentration des espèces chimiques réellement présentes dans une solution : on place le symbole de l’espèce chimique entre crochets [X].
Pour une espèce chimique X présente dans la solution, c’est la quantité de matière de X présente dans la solution divisée par le volume de la solution. $[X]=\frac{n(X)}{V_{\text {solution }}}$ l’unité de [X] est mol/L
Exemple
Soit la réaction de dissolution d’équation : $\mathrm{A}_\alpha \mathrm{B}_\beta \rightarrow \alpha \cdot \mathrm{A}^{\beta+}{ }_{(\mathrm{aq})}+\beta \cdot \mathrm{B}^{\alpha-}{ }_{(\mathrm{aq})}$
Les concentrations effectives des espèces chimiques (ions) en solution sont : $\left\{\begin{array}{l}{\left[\mathrm{A}^{\beta+}\right]=\alpha \cdot \mathbf{C}} \\ {\left[\mathbf{B}^{\alpha-}\right]=\beta . \mathbf{C}}\end{array}\right.$ avec $\mathbf{C}$ la concentration de la solution $\mathbf{C}=\frac{n\left(A_\alpha B_\beta\right)}{V_s}$
