Energie thermique et Transfert thermique.
Introduction :
I. AUTRES EFFETS DU TRAVAIL :
Le travail reçu par un corps peut :
- le déformer. ex : lorsqu’on tend un arc, il se déforme ce qui modifie les interactions microscopiques entre les particules qui constituent l’arc.
Cette déformation de l’arc entraîne une mise en réserve d’énergie qui pourra être cédée à la flèche. - élever sa température: ex : forces de frottement d’un frein sur une roue de vélo.
- le déformer. ex : lorsqu’on tend un arc, il se déforme ce qui modifie les interactions microscopiques entre les particules qui constituent l’arc.
L’augmentation de la température traduit une plus grande agitation microscopique ( donc une augmentation de l’énergie cinétique microscopique).
- le faire changer d’état : ex : Le travail des forces de frottement des skis sur la neige entraîne la fusion de la neige, donc une modification des interactions microscopiques.
Dans les 3 cas, l’énergie reçue par le corps sous forme de travail à modifié les interactions microscopiques entre les particules.
Comme à l’échelle macroscopique, on peut définir à l’échelle microscopique une énergie cinétique due à l’agitation des particules et une énergie potentielle d’interaction due aux positions des particules en interaction.
Cette énergie microscopique d’origine cinétique et potentielle est appelée énergie interne du système. notée U.
$$
\mathrm{U}=\mathrm{E}_{\text {Cmicroscopique }}+\mathrm{E}_{\text {Pmicroscopique }}
$$
II. TRANSFERT THERMIQUE :
1. effets d’un transfert thermioue:
Exemple: On chauffe de l’eau, sa température augmente puis lorsqu’on atteint $100^{\circ} \mathrm{C}$, il y a changement d’état. L’augmentation de la température de l’eau et son changement d’état entraînent une modification de l’énergie interne.
Cette variation d’énergie interne est due à un transfert d’énergie appelé chaleur et noté $\mathbf{Q}$ (en Joule)
2. comment s’effectue un transeert thermioue?
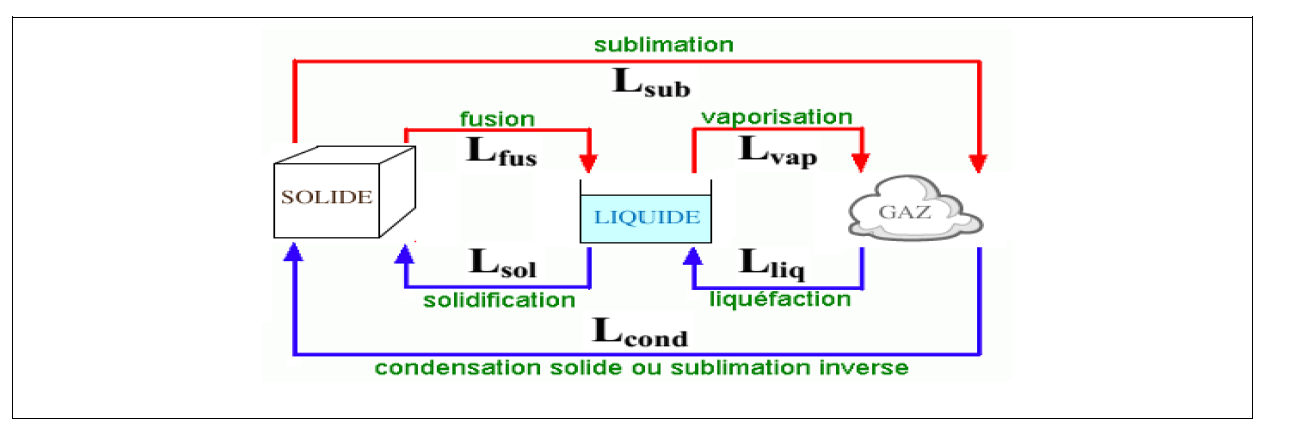
Il s’effectue toujours du corps le plus chaud vers le corps le plus froid, . Ce transfert peut se faire par :
- conduction: la conduction est un mode de transfert thermique qui
s’effectue sans transport de matière - convection : déplacement sous forme de courant ( air chaud : il
s’élève au dessus de la source chaude).
La convection est un mode de transfert qui s’effectue avec transport
de matière.- rayonnement : ex:les ondes électromagnétiques émises par le
soleil chauffent la Terre. Ce transfert d’énergie s’appelle
rayonnement (ou radiation).
- rayonnement : ex:les ondes électromagnétiques émises par le
- conduction: la conduction est un mode de transfert thermique qui
3. l’enceinte adiabatique
C’est toute enceinte qui ne permet pas les échanges thermiques avec le milieu extérieur. Exemples: bouteille thermos, calorimètre.
4.Le premier principe de la thermodynamique
L’énergie transférée à un corps sous forme de travail peut modifier son énergie interne et on écrit : $\underline{\Delta U}=\mathrm{W}$. L’énergie transférée à un corps sous forme de chaleur peut modifier son énergie interne et on écrit : $\underline{\Delta U=Q}$. D’une façon générale $\Delta \mathbf{U}=\mathbf{W + Q}$ et qui est l’expression mathématique du premier principe de la thermodynamique
5. Les signes conventionnels
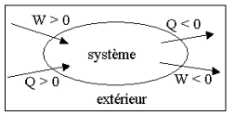
Soit W l’énergie transférée à un système sous forme de travail des forces extérieures et Q l’énergie transférée sous forme thermique. Ces grandeurs sont algébriques.
Ce que reçoit le système est compté positivement et ce qu’il cède est compté négativement.
6. La transformation cyclique
Durant cette transformation l’état initial est identique à l’état final.
On a
$\begin{gathered}\Delta U=W+Q \\ U_f-U_1=W+Q \\ 0=W+Q \\ W=-Q\end{gathered}$
Donc si le système reçoit de l’énergie sous forme de chaleur il la restitue sous forme de travail et vis versa.
7. L’equilibre thermique
On place deux corps A et B de températures différentes $\mathrm{T}_{\mathrm{A}}>\mathrm{T}_{\mathrm{B}}$ dans un calorimètre.

Le transfert thermique se produit entre les corps jusqu’à ce que la température se stabilise à la valeur T Qui s’appelle la température d’éguilibre thermique.
Soit $\Delta U_A$ la variation d’énergie interne du corps $A \quad: \Delta U_A=Q_A$.
Soit $\Delta U_B$ la variation d’énergie interne du corps $B: \Delta U_B=\mathrm{Q}_{\mathrm{B}}$.
Soit $\Delta U_C$ la variation d’énergie interne du calorimètre : $\Delta U_c=Q_C$.
la variation d’énergie du système est : $\Delta U=\Delta U_A+\Delta U_B+\Delta U_C$ et puisque système n’échange ni chaleur ni travail avec l’extérieur $\Delta U=0$ on en déduit : $\mathbf{Q}_{A+} \mathbf{Q}_B+\mathbf{Q}_C=\mathbf{0}$ cette relation s’appelle la relation calorimétrique,
III. Transfert thermique et energie thermique
1.Transfert par chaleur produisant une élevation de température.
1.1 Energie thermique – quantité de chaleur
Au cours du transfert thermique l’expression de l’énergie thermique ou quantité de chaleur $\mathbf{Q}$ échangée d’un système sans changement d’état est donnée par la relation :
Q=m \cdot C \cdot\left(\theta_{\mathrm{f}}-\theta_i\right)
avec: Q en J (Joule);
m : masse en kg ;
C : chaleur massique en $\mathrm{J} \cdot \mathrm{kg}^{-1} .{ }^{\circ} \mathrm{C}^{-1}$;
$\theta_{\mathrm{f}}$ et $\theta_{\mathrm{i}}$ : températures finale et initiale en degré Celsius $\left({ }^{\circ} \mathrm{C}\right)$
1-2 La chaleur massique
La chaleur massique $\mathbf{C}$ est la quantité de chaleur nécessaire pour faire varier de $1^{\circ} \mathrm{C}$ ou $1^{\circ} \mathrm{K}$, une unité de masse de 1 kg d’un liquide, d’un gaz ou d’un solide. «Plus C est petit, plus il chauffera vite.» C s’exprime en J. $\mathrm{kg}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}\left(\mathrm{ou} \mathrm{J} \cdot \mathrm{kg}^{-1} \cdot \mathrm{~K}^{-1}\right)$
La capacité thermique $\boldsymbol{\mu}$ d’un corps de masse $m$ est la quantité de chaleur (énergie thermique) qu’il faut lui fournir pour augmenter sa température de $1^{\circ} \mathrm{C}$ ou $\left(1^{\circ} \mathrm{K}\right)$. avec $\mu=\mathrm{m} . \mathrm{C}$ s’exprime en $\mathrm{J}^{\circ}{ }^{\circ} \mathrm{C}^{-1}\left(\right.$ ou J. $\left.\mathrm{K}^{-1}\right)$
Exemples
| Corps état physique | État physique | C (J·kg⁻¹·K⁻¹) |
|---|---|---|
| Diazote | gaz | 1040 |
| Ethanol | liquide | 2460 |
| Zinc | solide | 417 |
| Eau | gaz | 1850 |
| Eau | liquide | 4186 |
| Eau | solide | 2060 |
2. Transfert d’énergie produisant un changement d’état
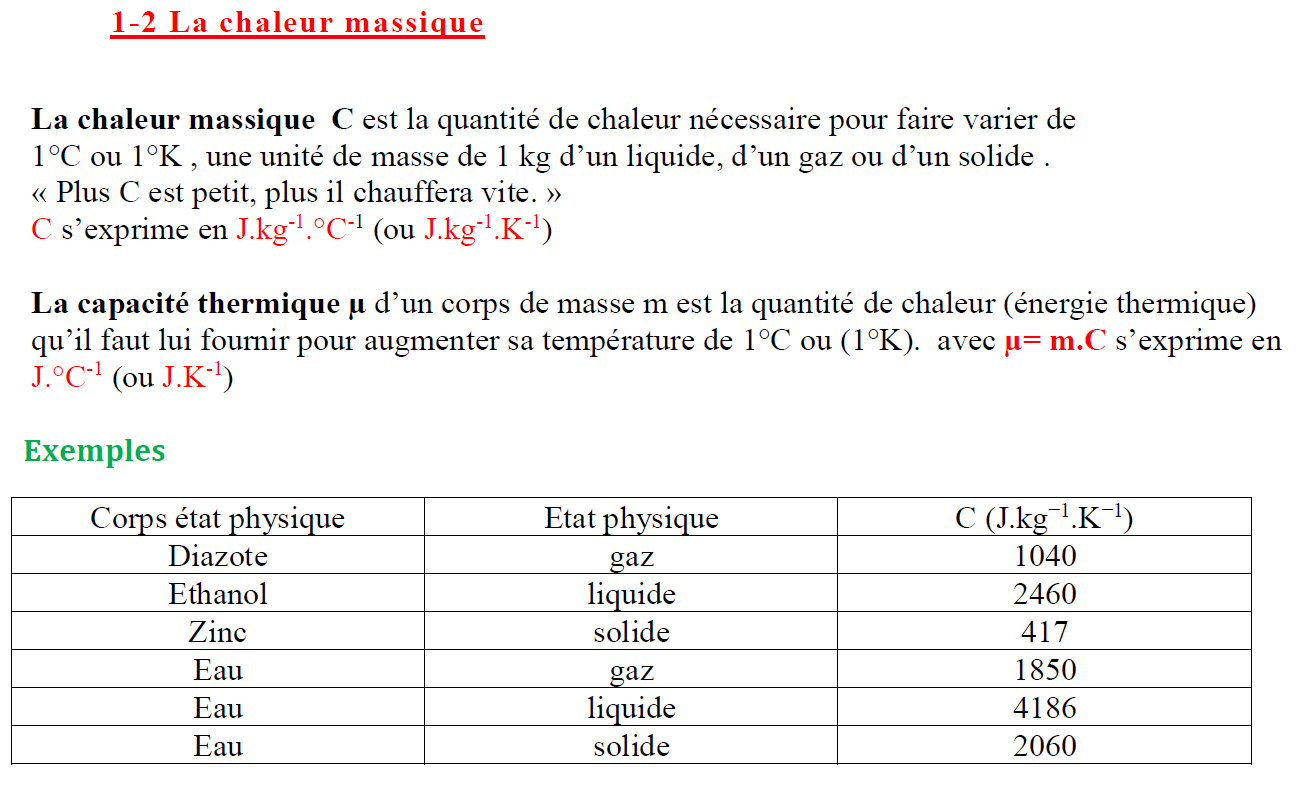
2.1 Les différents changemants d’état
Définition: Un changement d’état physique correspond au passage d’un état physique à un autre état physique. Il se fait à température constante,

2.2 L’énergie thermique de changement d’état : chaleur latente
– La chaleur latente de changement d’état, notée $\mathbf{L}$, est l’énergie qu’il faut fournir à 1 kg d’un corps pur (liquide, solide ou gaz), à sa température de changement d’état, pour qu’il change d’état.
Exemple:
chaleur latente de fusion de l’eau glace : $\mathrm{L}_{\text {fus }}=334 \cdot 10^3 \mathrm{~J} \cdot \mathrm{~kg}^{-1}$
chaleur latente de vaporisation de l’eau liqude : $\mathrm{L}_{\text {vap }}=2,26 \cdot 10^6 \mathrm{~J} \cdot \mathrm{~kg}^{-1}$
Lors de son changement d’état, la masse $m$ d’un corps pur échange avec l’extérieur l’énergie:
$$
\mathbf{Q}=\mathbf{m} \cdot \mathbf{L}_{\text {chang }}
$$
Q : énergie thermique échangée en joule (J)
$\mathbf{m}$ : masse du corps en kilogramme (kg)
$$\mathbf{L}_{\text {chang }} $$: chaleur latente de changement d’état en joule par kilogramme $\left(\mathrm{J} \cdot \mathrm{kg}^{-1}\right)$
Remarque: $L_{\text {sol }}=-L_{\text {fus }} ; L_{\text {cond }}=-L_{s u b} ; \quad L_{i l q}=-L_{v a p}$