Ondes mécaniques progressives
Objectifs :
À l’issue de cette leçon, l’élève sera capable de :
1. Définir une onde mécanique et sa célérité.
2. Identifier et différencier une onde transversale d’une onde longitudinale.
3. Définir ce qu’est une onde progressive.
4. Appliquer la relation entre l’élongation d’un point du milieu de propagation et l’élongation de la source : \( y_M(t) = y_S(t – r) \).
5. Exploiter la relation entre le retard temporel, la distance et la célérité d’une onde mécanique.
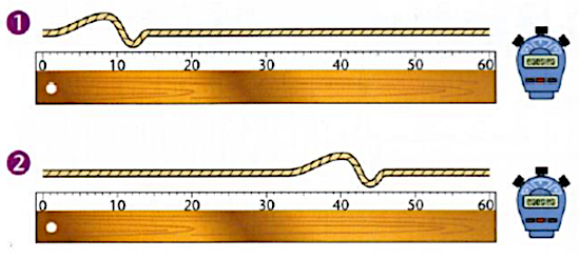
6. Analyser des données expérimentales pour déterminer la distance, le retard temporel et la célérité.
7. Proposer un montage expérimental pour mesurer le retard temporel ou la célérité lors de la propagation d’une onde.
1. Onde Mécanique et de sa Célérité
1.1. Onde mécanique :
Definition:
Une onde mécanique est une perturbation qui se propage dans un milieu matériel (solide, liquide ou gaz) sans transporter de matière, mais en transportant de l’énergie.
Ce type d’onde nécessite un support pour se propager, contrairement aux ondes électromagnétiques qui peuvent se propager dans le vide.
Le support de propagation peut être :
Un solide (comme une corde ou un rail),
Un liquide (comme l’eau),
Un gaz (comme l’air pour les ondes sonores).
Les ondes mécaniques peuvent se propager sous différentes formes, mais elles nécessitent une certaine élasticité et densité du milieu pour se propager.
Cette propagation se fait avec transport d’énergie et sans transport de matière.
Propriétés d’une onde:
Onde unidimensionnelle qui se propage dans une seule direction (la corde et le ressort)
Onde bidimensionnelle qui se propage dans un plan (la surface de l’eau)
Onde tridimensionnelle se propage dans l’espace (le son)
1.2. Célérité (Vitesse de propagation) :
Definition:
La célérité \( v \) d’une onde mécanique est la vitesse à laquelle l’onde se propage dans le milieu. Elle dépend des propriétés du milieu, telles que sa densité et son élasticité. La célérité est une grandeur scalaires mesurée en mètres par seconde (m/s).
Elle peut être calculée à partir de la relation :
\[
v = \frac{d}{t}
\]
où :
– \( v \) est la célérité en m/s,
– \( d \) est la distance parcourue par l’onde en mètres (m),
– \( t \) est le temps mis pour parcourir cette distance en secondes (s).
Exemple :
Si la distance entre le haut-parleur et le microphone est de 10 mètres, et que le retard temporel mesuré est de 0,03 secondes, la célérité de l’onde sonore dans l’air sera :
\[
v = \frac{d}{r} = \frac{10 \, \text{m}}{0,03 \, \text{s}} = 333,33 \, \text{m/s}
\]
Ce calcul donne une estimation de la célérité de l’onde dans l’air à température ambiante (environ 340 m/s, ce qui correspond à une vitesse du son dans l’air).
Remarque :
Pour l’onde sonore, la célérité augmente avec la densité du milieu de propagation.
$\mathrm{v}_{\mathrm{gax}}<\mathrm{v}_{\text {Bquide }}<\mathrm{v}_{\text {solide }}$
2. Ondes Transversales et Longitudinales
Les ondes mécaniques peuvent être classées en transversales et longitudinales, selon la direction dans laquelle les particules du milieu se déplacent par rapport à la direction de propagation de l’onde.
2.1. Onde Transversale :
Dans une onde transversale, la direction de la perturbation est perpendiculaire à la direction de propagation de l’onde.
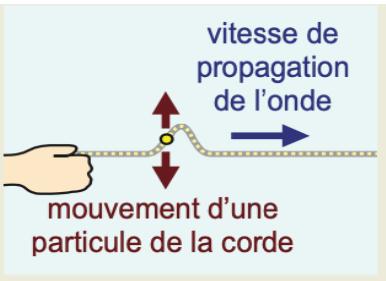
Exemple :
Les vagues à la surface de l’eau ou les vibrations d’une corde de guitare lorsqu’elle est pincée.
Les particules du milieu se déplacent de haut en bas (perpendiculairement) à la direction de l’onde qui se déplace horizontalement.
2.2. Onde Longitudinale :
Dans une onde longitudinale, la direction de la perturbation est parallèle à la direction de propagation de l’onde.
Exemple :
Le son dans l’air est une onde longitudinale. Dans ce cas, les particules de l’air se déplacent dans la même direction que celle de la propagation de l’onde.
Les particules du milieu vibrent alternativement en compressant et en dilatant la matière, créant ainsi des zones de compression et de rarefaction.
3. Onde Mécanique Progressive
3.1.Définition
Une onde progressive est une onde qui se propage dans un milieu matériel, transportant de l’énergie sans transporter de matière.
Dans le cas d’une onde mécanique progressive, chaque point du milieu effectue une oscillation autour de sa position d’équilibre, mais c’est l’énergie de la perturbation qui se déplace d’un endroit à un autre, et non les particules du milieu.
La progression se fait dans une direction bien précise, c’est-à-dire que la perturbation se déplace au fil du temps.
Exemple :
Lorsqu’une pierre tombe dans un étang, elle génère des ondes circulaires à la surface de l’eau. Ces ondes sont progressives, transportant de l’énergie à travers l’eau sans déplacer la matière de manière permanente.
3.2. Vitesse de propagation
Les ondes se propagent dans les milieux homogènes avec une vitesse constante, qui dépend des propriétés du milieu (l’élasticité et l’inertie) et s’exprime par le rapport de la distance (d) parcourue par l’onde pendant une durée (Δ𝒕), tel que:
V = d/Δ𝒕
Exemple:
La vitesse d’une onde se déplaçant le long d’une corde dépend de la masse linéique de la corde μ et de sa tension F : $\mathrm{V}=\sqrt{\frac{F}{\mu}}$
avec : μ=m/L est la masse linéique de la corde.
La vitesse d’une onde sonore dans un gaz :
$\mathrm{V}=\sqrt{\frac{\gamma \cdot P}{\rho}}$
γ est une constante sans unité qui caractérise le gaz . P : la pression ; ρ : la masse volumique
Si le gaz est considéré parfait :
$\mathrm{V}=\sqrt{\frac{Y \cdot R T}{M}}$
Remarque : Pour l’onde sonore, la célérité augmente avec la densité du milieu de propagation.
$\mathrm{v}_{\mathrm{gax}}<\mathrm{v}_{\text {Bquide }}<\mathrm{v}_{\text {solide }}$
Exercices :
Détection sous-marine :
Une explosion a lieu 50 m au-dessus de la surface de la mer. La vitesse du son est d’environ 340m/s dans l’air et de 1500 m/s dans l’eau.
Au bout de combien de temps, un sous-marin situé exactement sous le point d’explosion à 30 m de profondeur, détecte-t-il le bruit d’explosion ?
Célérité du son dans l’acier :
Sur un chantier, un ouvrier frappe un coup à l’extrémité d’une tige en acier de 100 m de long.
Un second ouvrier, situé à l’autre extrémité de la poutre, entend alors 2 coups successifs. La célérité du son dans l’air est de 340 m/s.
1- Expliquer pourquoi l’ouvrier entend deux coups.
2- Sachant que la durée qui sépare les deux coups est de 0,277s, calculer la célérité de
l’onde dans l’acier de la tige.
4. Propriétés d’une ondes mécanique
4.1. Le retard temporel
Definition:
Le retard temporel d’un point N par rapport à point M est le temps nécessaire à l’onde pour traverser la distance MN, on le note τ .
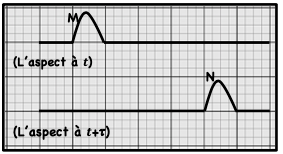
On a $v=\frac{M N}{\tau}$ donc $\tau=\frac{M N}{v}$
4.2. L’élongation d’un point M
Definition:
L’élongation d’un point est la distance d’évolution de ce point autour de sa position d’équilibre on la note $y$.
y est une valeur algébrique, sa valeur maximum est appelée amplitude.
Remarques:
* L’élongation y dépend du temps et de la position par rapport à la source $S$, donc $y=f(x, t)$ avec $\mathrm{x}=\mathrm{SM}$.
* Chaque point refait le même mouvement de la source $S$ mais après un retard $\tau$
$$
y_{\mathrm{M}}(t)=y_{\mathrm{s}}(t-\tau) \text { ou } y_{\mathrm{S}}(t)=y_{\mathrm{s}}(t+\tau) \text {. }
$$
* À un instant $t_1$ donné, $y=f(x)$ présente l’aspect (l’image) de l’onde á cet instant.
On a $v=\frac{M N}{\tau}$ donc $\tau=\frac{M N}{v}$
La longueur de l’onde: $\mathrm{L}=\frac{Q F}{t_1-t_0}$
$F$ : le front d’onde; $Q$ : la queue de l’onde; $L=Q F$
* Pour un point $M_1\left(x_1=c t e\right), y_{M_1}=f(t)$ présente la variation de l’élongation de $M_1$ en fonction du temps.
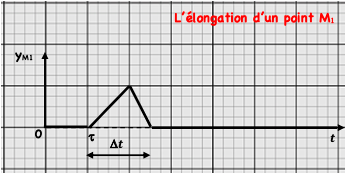
On a $V=S M_1 / \tau$ ou $V=L / \Delta t$
avec:
$\tau$ : Le retard temporel
$\Delta t$ : la durée de l’onde
Ce test a pour objectif de vous aider à consolider vos connaissances sur les principes fondamentaux des ondes. Vous allez explorer des notions telles que la définition d’une onde mécanique, la distinction entre ondes transversales et longitudinales, ainsi que les concepts de célérité, de retard temporel et d’élongation.
Ce quiz inclut également des questions pratiques qui vous permettront de mettre en application ces concepts dans des situations réelles.
Prenez le temps de bien lire chaque question avant de répondre, et bonne chance !
Exercice d’application :
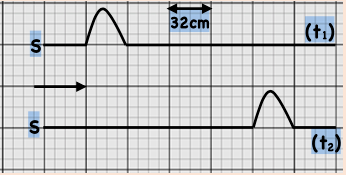
La figure ci-dessous représente l’aspect d’une corde tendue à deux instants différents $𝒕_1=0,6s$ et $ 𝒕_2 =1,4s$.
1- Calculer la célérité de l’onde le long de la corde.
2- Déduire la durée de déformation.
3- À quel instant la perturbation a- t-elle commencé sa propagation à partir de la source ?
4- Représenter l’aspect de la corde à l’instant 𝒕3 = 1,28s
