Travail et Energie potentielle de pesanteur- énergie mécanique.
Introduction :
I. ENERGIE POTENTIELLE DE PESANTEUR
1. Notion d’énergie potentielle de pesanteur
L’énergie potentielle de pesanteur d’un solide est une énergie due à sa position par rapport à la Terre. Elle dépend de l’altitude de son centre d’inertie G.
Exemple
l’eau d’un barrage, immobile et stockée en altitude, possède de l’énergie en réserve du fait de sa position par rapport à la Terre : elle possède de l’énergie potentielle. Si l’eau est libérée, cette énergie potentielle va se transformer en énergie cinétique au cours de la chute et l’eau pourra par exemple faire tourner la turbine d’un alternateur dans une centrale hydraulique.
2. Expression littérale de l’énergie potentielle de pesanteur
Au voisinage de la Terre, l’énergie potentielle de pesanteur d’un solide de masse m est définie par:
$$
E_{p p}=\mathbf{m} \cdot \mathbf{g} \cdot \mathbf{z}+\mathbf{C}
$$
avec l’ axe Oz vertical et orienté vers le haut.
Epp énergies potentielles de pesanteur du système en J;
m : masse du système en kg ;
g : intensité du champ de pesanteur en N.kg-1;
$z$ : cote du centre de gravité $G$ en $m$.
C est une constante arbitraire déterminée en choisissant un état de référence.
3. L’état de référence
L’état de référence est un état qu’on choisit arbitrairement et pour lequel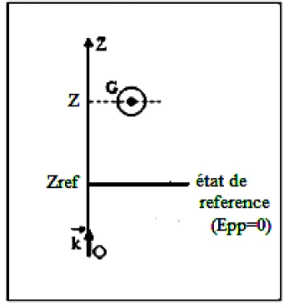
l’énergie potentielle est nulle.
Déterminons l’expression de l’énergie potentielle en choisissant :
l’état de référence : $E p p=0$ à $z=Z_{\text {ref }}$.
On a : $\mathrm{Epp}=\mathrm{mgz}+\mathrm{C}$
Donc: $0=\mathrm{mg} Z_{\text {ref }}+C$
D’où : $C=-m \cdot g \cdot Z_{\mathrm{ref}}$
L’expression de l’énergie potentielle devient:
$E p p=m \cdot g \cdot z-m \cdot g \cdot z_{\text {ref }}$
Donc: $\boldsymbol{E p p}=\boldsymbol{m} \cdot \boldsymbol{g} \cdot\left(\boldsymbol{z}-\boldsymbol{Z}_{\mathrm{ref}}\right)$
$E p p=m \cdot g \cdot \mathbf{z}$
\text { Si on prend } z_{\text {ref }}=0 \text { alors l’expression de l’énergie potentielle devient : } \boldsymbol{E p p}=\boldsymbol{m} \cdot \boldsymbol{g} \cdot \mathbf{z}
4. Variation de l’énergie potentielle de pesanteur
L’expression de la variation l’énergie potentielle du centre de gravité entre 2 points A et B est :
$$
\Delta \mathrm{Epp}=\mathrm{E}_{\mathrm{pp}}(\text { final })-\mathrm{E}_{\mathrm{pp}}(\text { initial })=\mathrm{E}_{\mathrm{pp}}(\mathrm{~B})-\mathrm{E}_{\mathrm{pp}}(\mathrm{~A})=\mathrm{mg}\left(\mathrm{Z}_{\mathrm{B}}-\mathrm{z}_{\mathrm{A}}\right)
$$
Or le travail de poids est $\mathrm{W}(\vec{P})=\mathrm{mg}\left(\mathrm{z}_{\mathrm{A}}-\mathrm{z}_{\mathrm{B}}\right)$
Donc $\Delta \mathrm{Epp}=\mathrm{E}_{\mathrm{pp}}($ final $)-\mathrm{E}_{\mathrm{pp}}($ initial $)=-\mathrm{W}(\vec{P})$
II. ENERGIE MECANIQUE
1. Définition d’energie mécanique
L’énergie mécanique $\mathbf{E}_{\boldsymbol{m}}$ d’un solide est égale à la somme de son énergie cinétique $\mathrm{E}_{\mathrm{c}}$ et de son énergie potentielle de pesanteur $\mathrm{E}_{\mathrm{pp}}: \mathbf{E}_{\mathbf{m}}=\mathbf{E}_{\mathbf{c}}+\mathbf{E}_{\mathrm{pp}}$ Elle s’exprime en joule (J).
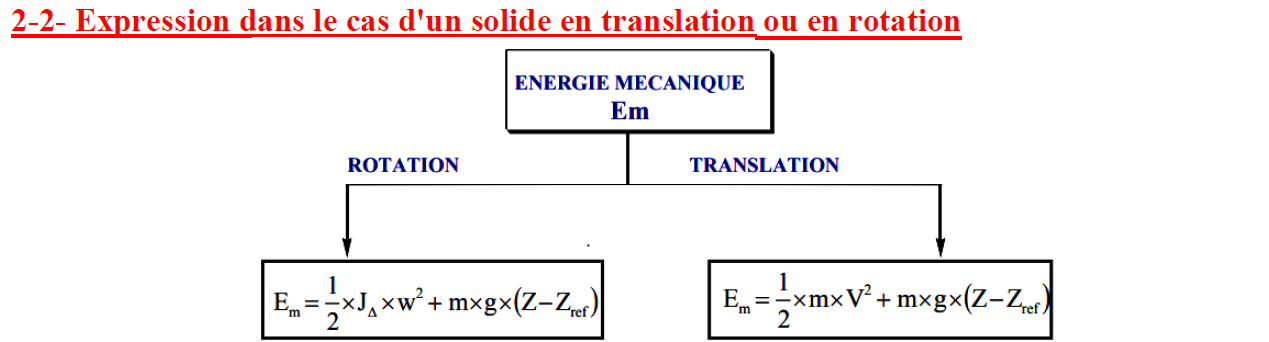
2. Expression dans le cas d’un solide en translation ou en rotation
3.Théorème de l’énergie mécanique
On a d’après le théorème del’énergiecinetique appliqué à un solide ayant unmouvement quelconque
$\begin{aligned} & \Delta \mathrm{E}_{\mathrm{C}}=\mathrm{W}(\overrightarrow{\mathrm{P}})+\sum \mathrm{W}\left(\overrightarrow{\mathrm{F}}_{\mathrm{n} . \mathrm{c}}\right) \\ & \Delta \mathrm{E}_{\mathrm{C}}=-\Delta \mathrm{E}_{\mathrm{pp}}+\sum \mathrm{W}\left(\overrightarrow{\mathrm{F}}_{\mathrm{ncc}}\right) \\ & \Delta \mathrm{E}_{\mathrm{C}}+\Delta \mathrm{E}_{\mathrm{pp}}=\sum \mathrm{W}\left(\overrightarrow{\mathrm{F}}_{\mathrm{nc}}\right)\end{aligned}$
$\overrightarrow{\mathrm{F}}_{\mathrm{n} . \mathrm{c}}$ : force non conservative
♠ Toute force constante est conservative (ex : poids, force électrique).
♠ Entre autres, les forces de frottements sont non conservatives.
$\Delta \mathrm{E}_{\mathrm{m}}=\sum \mathrm{W}\left(\overrightarrow{\mathrm{F}}_{\mathrm{n} . \mathrm{c}}\right)$
a.Conservation de l’énergie mécanique dou solide
Quand le poids est la seule force à travailler: $\sum \mathrm{W}\left(\overrightarrow{\mathrm{F}}_{\mathrm{n} . \mathrm{c}}\right)=0$
done :
$\Delta E_m=0$
done:
$\underline{E}_{\mathrm{m}}=$ Constante
L’énergie mécanique du solide reste donc constante on dit qu’elle se conserve et que le système étudié est conservatif.
De plus, On a $\Delta \mathrm{E}_{\mathrm{m}}=0$
donc $\Delta \mathrm{E}_{\mathrm{C}}+\Delta \mathrm{E}_{\mathrm{pp}}=0$
donc $\Delta \mathrm{E}_{\mathrm{C}}=-\Delta \mathrm{E}_{\mathrm{pp}}$
donc si $\Delta \mathrm{E}_{\mathrm{C}}>0$ alors $\Delta \mathrm{E}_{\mathrm{pp}}<0$ et vis versa .
donc si Ec augmente alors Epp diminue et vis versa.
c-à-d qu’il y a transformation de l’énergie cinétique en énergie potentielle
et vis versa.
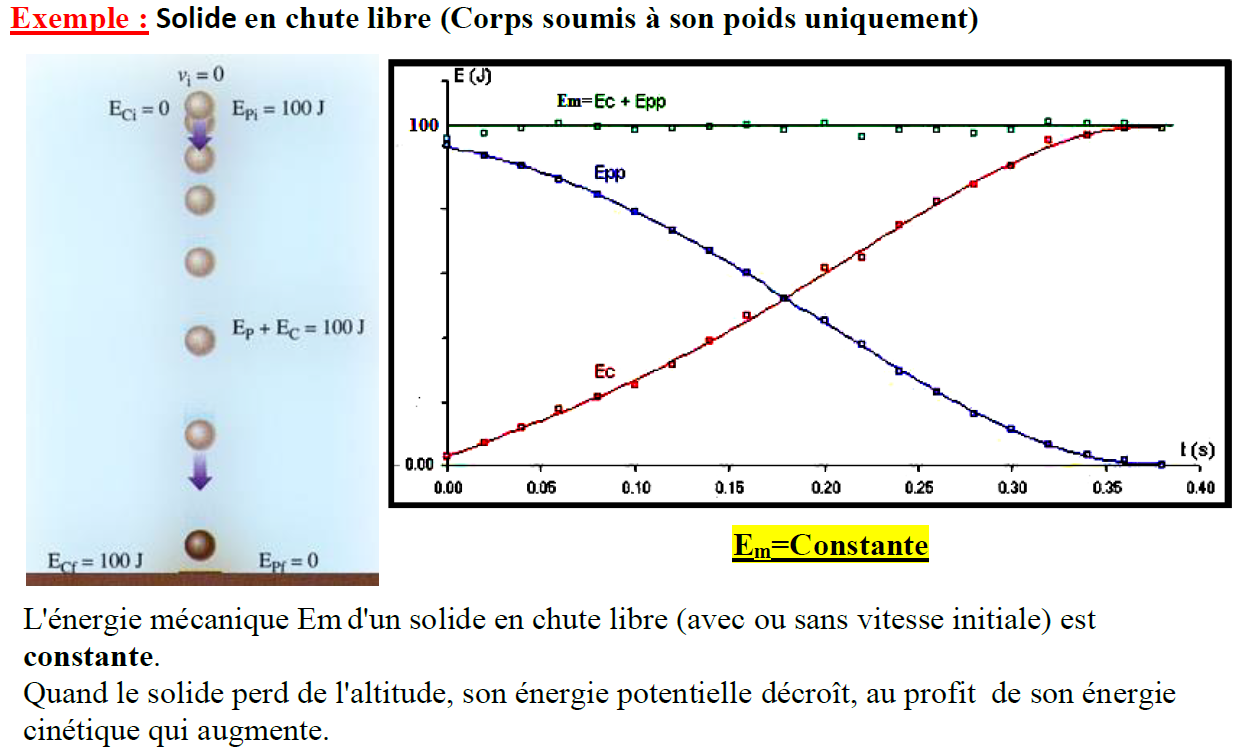
Exemple : Solide en chute libre (Corps soumis à son poids uniquement)
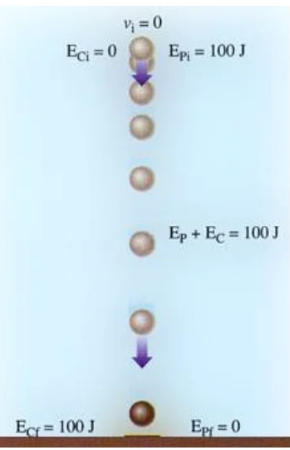
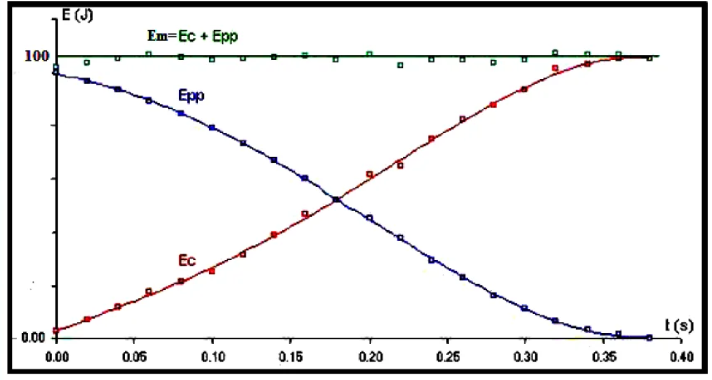
$\underline{E}_{\mathrm{m}}=$ Constante
L’énergie mécanqque Em d’un solide en chute libre (avec ou sans vitesse initiale) est constante.
Quand le solide perd de l’altitude, son énergie potentielle décroît, au profit de son énergie cinétique qui augmente.
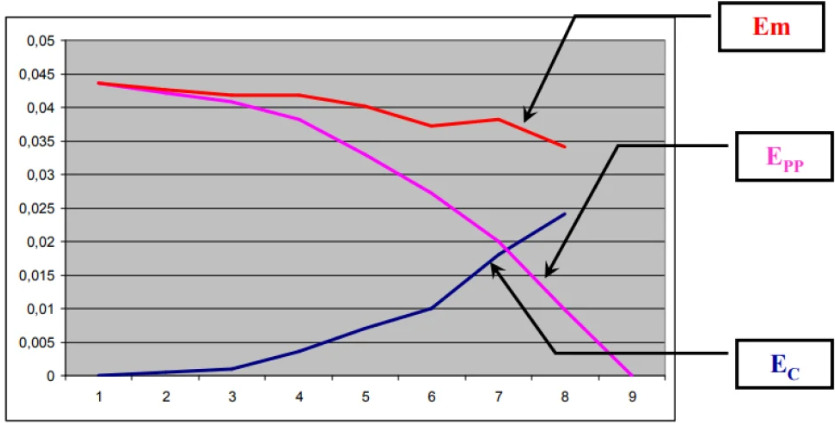
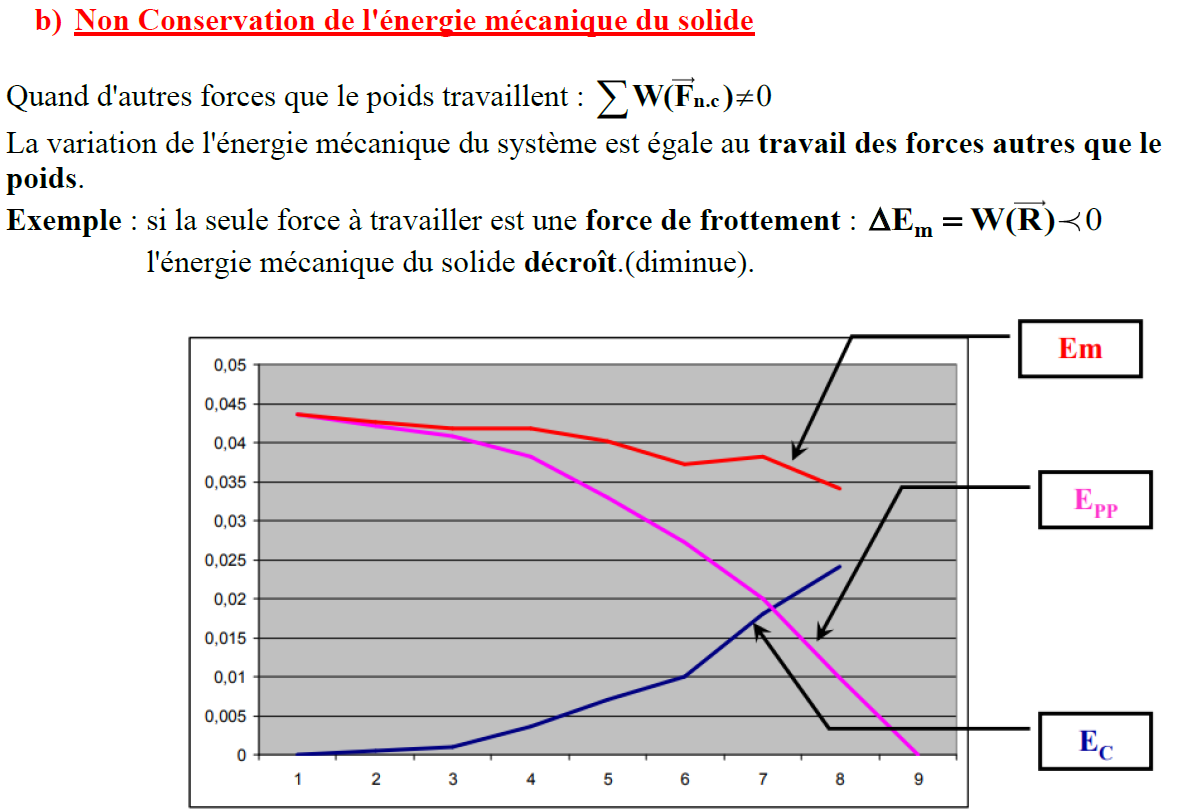
b. Non Conservation de l’énergie mécanique du solide
Quand d’autres forces que le poids travaillent : $\sum \mathbf{W}\left(\overrightarrow{\mathbf{F}}_{\mathbf{n c c}}\right) \neq 0$
La variation de l’énergie mécanique du système est égale au travail des forces autres que le poids.
Exemple : si la seule force à travailler est une force de frottement : $\Delta \mathbf{E}_{\mathrm{m}}=\mathbf{W}(\overrightarrow{\mathbf{R}}) \prec 0$ l’énergie mécanique du solide décroît.(diminue).
