Transformations nucléaires spontanées
I. Le noyaux d'un atome
1) Les constituants d’un noyau.
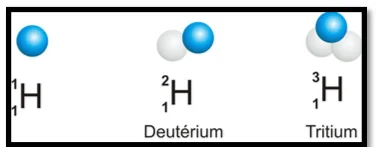
Un atome est constitué d’un noyau de diamètre de l’ordre de $10^{-15} \mathrm{~m}$ ( 1 fm – fentométre) et $d^{\prime}$ électrons formant le nuage électronique autour de ce noyau.
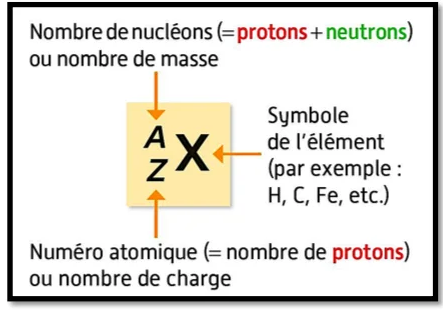
Le noyau appelé aussi nucléide est constitué de protons et de neutrons appelé nucléons On le note :
2) Les isotopes
Les isotopes sont des nucléides de même nombre de masse et de nombre de charge différant. Donc un nombre de neutron différant.
II. la vallée de stabilité dans le diagramme de Segré
1) La radioactivité
La radioactivité est une transformation nucléaire spontanée et aléatoire au cour du quelle un noyau instable se transforme en noyau plus stable avec émission d’un rayonnement nucléaire.
2) Les noyaux stables
( » vallée de la stabilité » la zone rouge)
Pour $\mathbf{Z}<20$, les noyaux stables se situent au voisinage d’une droite $Z=N$
Pour $Z>20$, le nombre de neutrons augmente plus vite que le nombre de protons, les noyaux se situent au-dessus de cette droite.
Le diagramme de Sergé : N=f(Z)
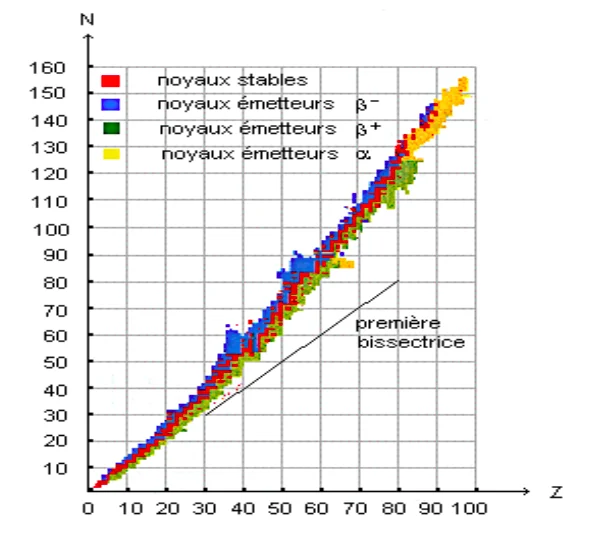
3) Les noyaux instables
On distingue 3 types :
↬1er type
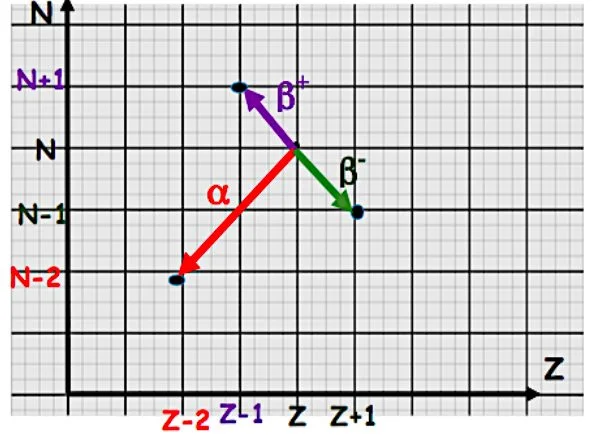
a- les noyaux qui ont un excès de neutrons (au-dessus de la vallée de stabilité zone bleu ), Ces noyaux se désintègrent avec émission d’un électron ${ }_{-1}^0 e$.
On dit que ces noyaux ont une radioactivité $\beta$-.
b- les noyaux qui ont un excès de protons (au-dessous de la vallée de stabilité zone verte ),
Ces noyaux se désintègrent avec émission d’un positron ${ }_{+1}^0 e$.
On dit que ces noyaux ont une radioactivité $\beta+$.
↬3 ème type
c- Noyaux ayant un défaut de neutrons et dont le nombre A > 200 (noyau lourd, zone jaune)
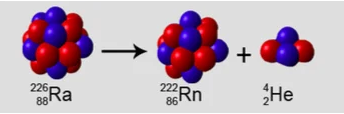
Ces noyaux se désintègrent avec émission d’un noyau d’hélium ${ }_2^4 \mathrm{He}$.
On dit que ces noyaux ont une radioactivité $\alpha$.
III. Les transformations nucléaires spontanées.
1. Les lois de conservations (lois de soddy )
Au cours d’une transformation nucléaire, il y a conservation du nombre $A$ et du nombre $Z$.
$$
{ }_Z^A \boldsymbol{X} \longrightarrow{ }_{Z_1}^{A_1} \boldsymbol{Y}+{ }_{Z_2}^{A_2} \boldsymbol{x}
$$
$X$ est le noyau père, $Y$ est le noyau fils et $x$ est le rayonnement nucléaire.
Ona: $A=A_1+A_2$ et $Z=Z_1+Z_2$
2. Les réactions nucléaires
• $$
\text { – Désintégration } \alpha \quad{ }_Z^A X \rightarrow{ }_{Z-2}^{A-4} Y+{ }_2^4 \mathrm{He}
$$
• $$
\text { Désintégration } \beta . \quad{ }_Z^A X \rightarrow{ }_{Z+1}^A Y+{ }_{-1}^0 e
$$
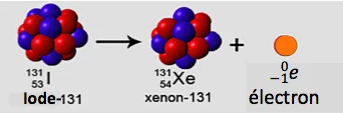
au cours de cette réaction un neutron se transforme en proton avec l’émission d’un électron.
Donc le mécanisme de cette réaction est : ${ }_0^1 n \longrightarrow{ }_1^1 p+{ }_{-1}^0 e$
• Désintégration $\beta^{+} . \quad{ }_Z^A X \rightarrow{ }_{Z-1}^A Y+{ }_1^0 e$
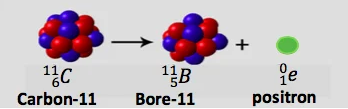
au cours de cette réaction un proton se transforme en neutron avec l’émission d’un positron.
Donc le mécanisme de cette réaction est : ${ }_1^1 p \longrightarrow{ }_0^1 n+{ }_1^0 e$
Les transformations nucléaires sur le diagramme de segré
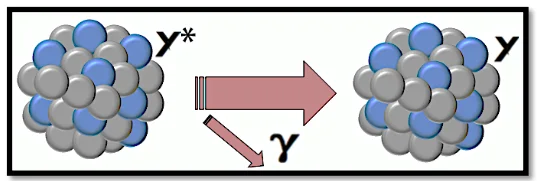
La désexcitation: le noyau fils excité se désexcite pour donner une radiation magnétique formée par un photon $\left({ }_0^0 \gamma\right)$.
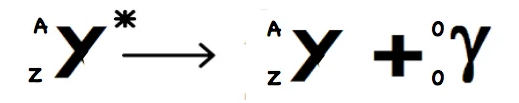
Remarque
Un photon est une particule sans masse ni charge et qui a une énergie proportionnelle à sa fréquence.
3. La famille radioactive
$C$ ‘est un série de nucléides descendant d’un même noyau radioactif , par une suite de désintégrations successives jusqu’à l’obtention d’un noyau stable.
VI. la décroissance radioactive
1) la lois de décroissance radioactive
Considérons un échantillon contenant $N(t)$ noyaux radioactifs à la date $t$. La variation du nombre de noyaux restants à l’instant $t$ (le nombre de noyaux désintégrés) pendant une durée dt est proportionnel à la durée dt et au nombre restant de nucléide N .
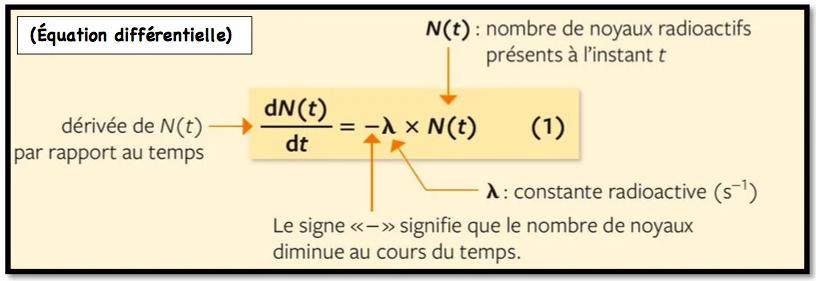
la solution de l’équation différentielle précédente s’écrie sous forme :

Remarque 1
le nombre de noyaux désintégrés à un instant $\dagger$ est $\mathbf{N}_{\mathrm{d}}=\mathbf{N}_0-\mathrm{N}$ ce qui donne
$$
N_{\mathrm{d}}=\mathrm{N}_{\mathrm{o}}\left(1-e^{-\lambda . t}\right)
$$
Remarque 2
$\lambda$ est une constante radioactive qui ne dépend que du nucléide. Elle est indépendante du temps, des conditions physiques et chimiques. son unité est sec ${ }^{-1}$ et elle représente aussi la probabilité de désintégration d’un noyau par unité de temps.
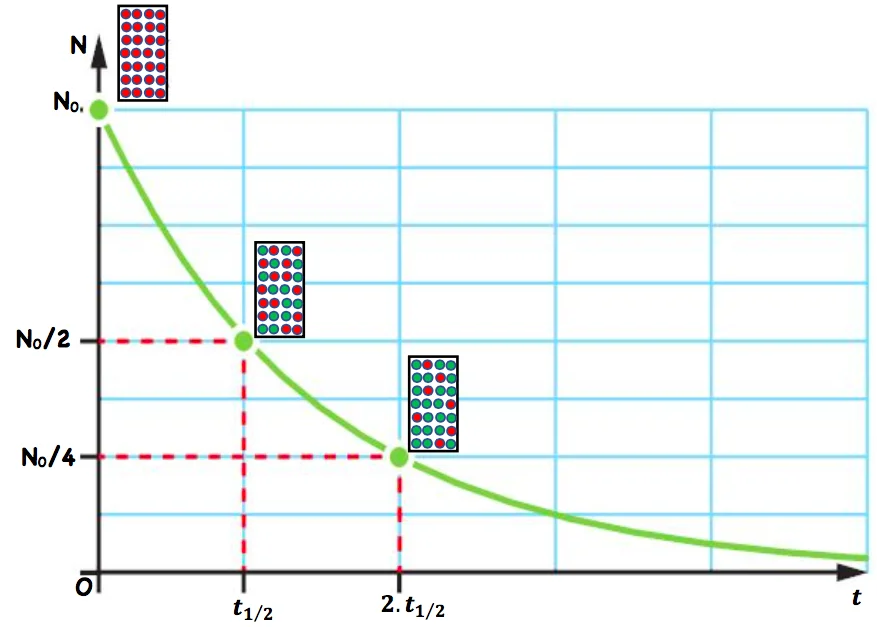
2) La demie vie (la période radioactive)
la demie vie $t_{1 / 2}$ est la durée au bout de laquelle la moitié des noyau radioactifs initialement présent dans l’échantillon se sont désintégrés.
$$
N\left(t_{1 / 2}\right)=\frac{N_O}{2} \Rightarrow \frac{1}{2}=e^{-\lambda+1 / 2} \quad \Rightarrow \quad t_{1 / 2}=\frac{\ln (2)}{\lambda}
$$
ーÉvolution du nombre de noyaux radioactifs
3) l’activité radioactive d’un échantillon.
L’activité radioactive $a(t)$ d’un échantillon radioactif à la date $t$ est le nombre de désintégrations par seconde de cet échantillon.
L’unité d’activité est le Becquerel Bq en hommage à Henri Becquerel $1 \mathrm{~Bq}=1$ désintégration par seconde $=1 \mathrm{~s}^{-1}$
on $a: a=-\frac{d N}{d t} \quad \Rightarrow \quad a=\lambda . N \quad \Rightarrow \quad a=a_0 e^{-\lambda t}$
V. La datation par le carbone-14.
Dès qu’un être vivant meurt, le carbone 14 n’est plus renouvelé : sa proportion se met à décroitre. Pour déterminer l’âge du matériau mort, on mesure l’activité $a(t)$ du carbone 14 d’un échantillon de matériau mort et $a_0$ l’activité du carbone 14 d’un échantillon de matériau identique encore vivant et on applique la formule: $a(t)=a_0 . e^{-\lambda t}$.
Ce qui donne :
$$
t=\frac{t_{1 / 2}}{\ln 2} \cdot \ln \frac{a_0}{a(t)}
$$
ou bien
$$
t=\frac{t_{1 / 2}}{\ln 2} \cdot \ln \frac{N_0}{N(t)}
$$
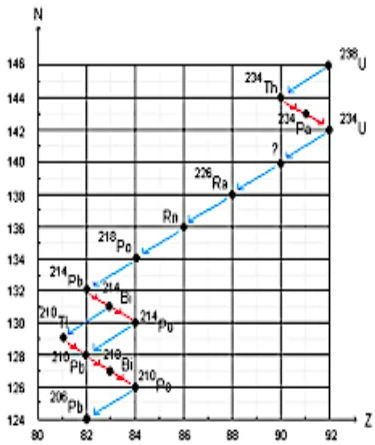
Après une série de désintégration successives de type $\alpha$ et $\beta$ – , le noyau ${ }_{92}^{238} U$ se transforme en ${ }_{82}^{206} P$. Déterminer le nombre de désintégration $\alpha$ et le nombre de désintégration $\beta^{-}$nécessaire pour cette transformation.
Le nucléide sodium $n^{24} \mathrm{Na}$ de radioactivité $\beta^{-}$qui donne un nucléide de magnésium $\mathrm{z}^{\mathrm{A}} \mathrm{Mg}$.
1. écrire l’équation de désintégration. Déterminer $\mathbf{A}$ et $\mathbf{Z}$.
2. Calculer la durée nécessaire pour que $75 \%$ de l’échantillon de sodium soit désintégré.
On donne : temps de demi-vie de nucléide sodium $t_{1 / 2}=15 \mathrm{~h}$
Le carbone ${ }_6^{14} \mathrm{C}$ et le carbone ${ }_6^{12} \mathrm{C}$ sont des nucléides présents dans l’atmosphère et dans tout organisme vivant dans des proportions sensiblement constantes (c’est à dire que le rapport du nombre de noyaux ${ }_6^{14} \mathrm{C}$ sur le nombre de noyaux ${ }_6^{12} \mathrm{C}$ est constant). Une fois que l’organisme cesse de vivre, le nombre de noyaux ${ }_6^{12} \mathrm{C}$ reste inchangé , par contre celui de noyaux ${ }_6^{14} \mathrm{C}$ décroît avec le temps par désintégration radioactive de type $\beta^{-}$de demi-vie $t_{1 / 2}=5570$ ans avec formation d’un noyau fils ${ }_Z^A X$.
$1^{\circ}$ Écrire l’équation de cette réaction de désintégration. Préciser le symbole du noyau fils ${ }_Z^A X$ en utilisant la liste suivante: ${ }_5^{12} \mathrm{~B},{ }_6^{13} \mathrm{C}, ~{ }_7^{13} \mathrm{~N},{ }_7^{14} \mathrm{~N},{ }_7^{15} \mathrm{~N}$.
$2^{\circ}$ Définir l’activité $a(t)$ d’un radioélément en précisant son unité dans le système international et établir son expression en fonction du temps.
$3^{\circ}$ Une épave d’une barque a été retrouvée récemment au large de la méditerrané. Dans le but d’estimer l’âge de cette barque, on en prélève un morceau de bois bien conservé. La mesure du nombre de désintégrations de noyaux ${ }_6^{14} \mathrm{C}$ donne 1307 désintégrations par minute. La même mesure effectuée sur un morceau de bois récent, de même nature et de même masse que celui utilisé précédemment, donne la valeur de 1720 désintégrations par minute. Déterminer l’âge de la barque.