Equivalence masse énergie
I. Équivalence masse-énergie
1) Postulat d’Einstein
Un système de masse m possède, lorsqu’il est au repos, une énergie appelée énergie de masse :
$$
\mathrm{E}=\mathrm{m} . \mathrm{c}^2 \quad\left\{\begin{array}{l}
E: \text { L’énergie en Joule } \\
m: \text { la masse du systéme en } \mathrm{kg} \\
C: \text { la célérité de la lumière dans } \\
\text { le vide en } m / s
\end{array}\right.
$$
2) Unités de masse et d’énergie
Dans le domaine de la physique nucléaire, le calcule d’énergie et de masse en unités du système international donne des valeurs très petites, donc il faut utiliser des unité plus adaptées.
Donc : pour l’énergie on utilise l’électronvolt ( eV ) avec :1 $\mathrm{eV}=1,6.10^{-19} \mathrm{~J} .\left(1 \mathrm{MeV}=1,6.10^{-13} \mathrm{~J}\right)$
Pour la masse on utilise l’unité de masse atomique « $u »:\left\{\begin{array}{l}1 u=1,66 \cdot 10^{-27} \mathrm{~kg} \\ 1 u=931,5 \mathrm{MeV} . \mathrm{C}^{-2}\end{array}\right.$
• I’unité de masse atomique (u) qui est égale à $1 / 12$ de la masse du ${ }^{12} C$.
• On a $E=m . C^2$ donc $m=E . C^{-2}$ ce qui permet d’exprimer la masse en Mev. $C^{-2}$.
II. Défaut de masse du noyau et énergie de liaison.
1) Défaut de masse d’un noyau
$$
\begin{aligned}
&\text { On a: }\\
&\begin{array}{|c|c|c|c|c|}
\hline \text { La particule } & \text { proton } & \text { neutron } & \text { électron } & \text { Helium-4 } \\
\hline \text { La masse en } u \text { u » } & 1,0073 & 1,0086 & 5,48.10^{-5} & 4,0015 \\
\hline
\end{array}
\end{aligned}
$$
La masse des constituants du noyau d’hélium-4 est : $2 . m(p)+2 . m(n)=4,0318 u$.
Donc on constate que la masse du noyau atomique est inférieure à la somme des masses des nucléons qui le constituent.
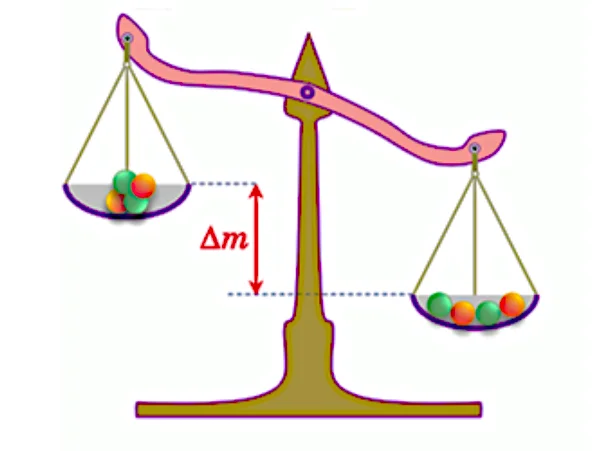
la différence entre eux est appelée défaut de masse noté $\Delta \mathrm{m}$.
Pour un nucléide ${ }_Z^A X$ le défaut de masse est :
$$
\Delta m=Z \cdot m_p+(A-Z) \cdot m_n-m(x)>0
$$
2) L’énergie de liaison d’un noyau.
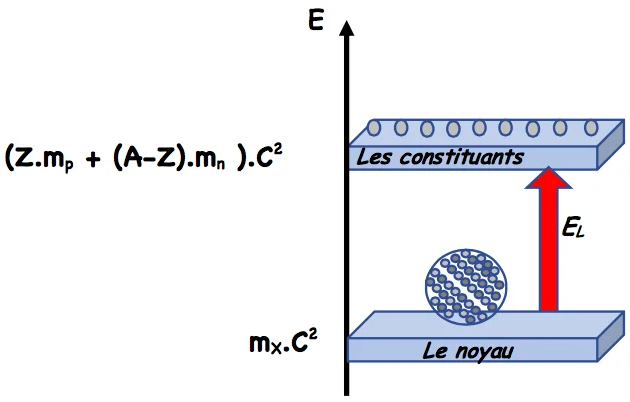
On appelle énergie de liaison d’un noyau l’énergie qui correspond au défaut de masse de ce noyau. $E_L=\Delta m \cdot C^2 \Rightarrow E_L=\left[Z \cdot m_p+(A-Z) \cdot m_n-m(x)\right] \cdot C^2$
L’énergie de liaison d’un noyau est l’énergie qu’il faut fournir à un noyau au repos pour le dissocier en nucléons isolés et immobiles.
3) L’énergie de liaison moyenne
C’est l’énergie de liaison par nucléon $\xi_L(X)=\frac{E_L}{A}$, on l’exprime en $\mathrm{MeV} /$ nucléon.
Avec A le nombre de nucléon du noyau
plus l’énergie ( $\xi_L$ ) est grande plus le noyau est stable.
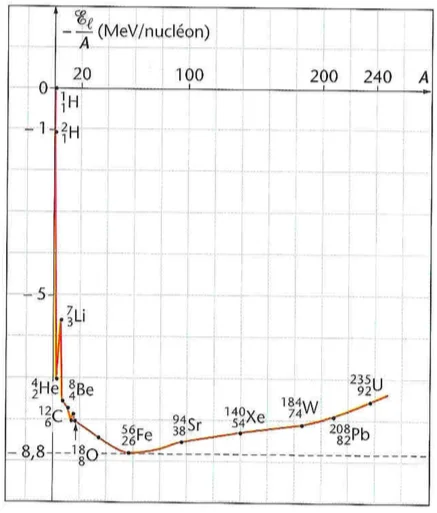
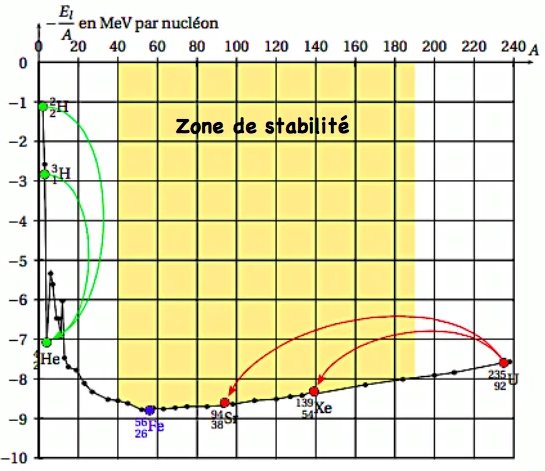
La courbe d’Aston donne l’évolution de l’opposé de l’énergie de liaison par nucléon (- $\xi_L$ ) en fonction de nombre de nucléons $A$ du noyau. Pour $40<A<150$, on constate que ( $-\xi_L$ ) prend des valeurs minimales qui correspondent aux noyaux plus stable.
III. l'énergie de réaction nucléaire
1) Définition
L’énergie d’une réaction nucléaire est l’énergie produite par la variation de masse entre les produits et les réactifs.
$$
\begin{aligned}
&\Delta \mathrm{E}=\Delta \mathrm{m} \cdot C^2\\
&\Delta m=m(\text { produits })-m(r e ́ a c t i f s)\langle 0 \text { pour les réactions exothermiques }\\
&\Delta E=[m(\text { produits })-m(\text { réactifs })] . C^2
\end{aligned}
$$
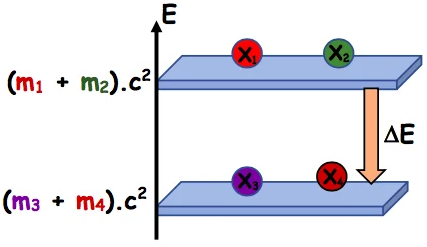
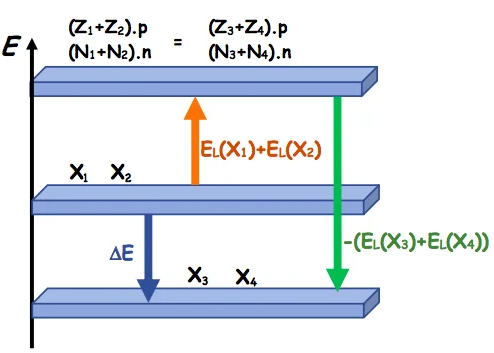
2) Diagramme énergétique.
$$
\begin{aligned}
&\text { Soit la réaction nucléaire suivante : } \quad{ }_{Z_1}^{A_1} X_1+{ }_{Z_2}^{A_2} X_2 \rightarrow{ }_Z^{A_3} X_3+{ }_{Z_3}^{A_4} X_3\\
&\Delta E=\left(m_3+m_4-m_1-m_2\right) \cdot c^2=\left(m_3+m_4\right) \cdot c^2-\left(m_1+m_2\right) \cdot c^2
\end{aligned}
$$
⊹ l’énergie libérée par une réaction est Elib= $|\Delta E|>0$
⊹Elib est l’énergie libérée par une seule réaction.
⊹ Pour $N$ nucléides réagi, l’énergie libérée est $E=N . E_{l i b}$
3) Bilan énergétique
$$
\begin{aligned}
&\text { Soit la réaction nucléaire suivante: }\\
&{ }_{Z_1}^{A_1} X_1+{ }_{Z_2}^{A_2} X_2 \rightarrow{ }_{Z_3}^{A_3} X_3+{ }_{Z_3}^{A_4} X_3\\
&\begin{aligned}
& E_L\left(X_1\right)=\left(Z_1 m_p+N_1 m_n-m\left(X_1\right)\right) \cdot c^2 \\
& E_L\left(X_2\right)=\left(Z_2 m_p+N_2 m_n-m\left(X_2\right)\right) \cdot c^2 \\
& E_L\left(X_3\right)=\left(Z_3 m_p+N_3 m_n-m\left(X_3\right)\right) \cdot c^2 \\
& E_L\left(X_4\right)=\left(Z_4 m_p+N_4 m_n-m\left(X_4\right)\right) \cdot c^2 \\
& \Delta E=\left(m_3+m_4-m_1-m_2\right) \cdot c^2
\end{aligned}\\
&\Delta E=E_L\left(X_1\right)+E_L\left(X_2\right)-E_L\left(X_2\right)-E_L\left(X_2\right)
\end{aligned}
$$
IV. Les réactions nucléaires provoquées.
1) la fission nucléaire
La fission nucléaire est une réaction nucléaire induite ou provoquée, au cours de laquelle un noyau fissile (Lourd) est bombardé par un neutron thermique, pour donner deux noyaux plus légers.
la réaction de fission libère de l’énergie.
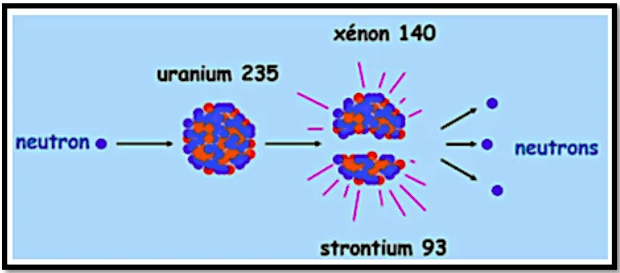
$$
{ }_0^1 n+{ }_{92}^{235} U \rightarrow{ }_{38}^{93} \mathrm{Sr}+{ }_{54}^{140} \mathrm{Xe}+3{ }_0^1 n .
$$
l’énergie libérer par la fission d’un noyau d’ ${ }^{235} \mathrm{U}$ est :
$$
E_{\text {Lib }}=|m(S r)+m(X e)+3 m(n)-m(U)-m(n)|=\left|E_L(U)-E_L(S r)-E_L(X e)\right|
$$
Remarques
⊹ La fission nucléaire est une réaction en
chaine. Elle produit des neutrons qui peuvent provoquer d’autre réactions de fission. Pour l’arrêter il faut ralentir les neutrons par des modérateurs comme l’eau lourde et des tige de graphite.
⊹ La réaction en chaine doit être contrôler pour qu’elle ne soit pas explosive (le cas de la bombe atomique). lorsque la fission est contrôlée, c’est le cas des réacteurs nucléaires où l’énergie est convertie en énergie électrique.
⊹ Un réacteur nucléaire transforme l’énergie nucléaire en énergie électrique avec un rendement :
$$
r=\frac{\mathcal{P}_{\text {elec }} \cdot \Delta t}{N . E_{\text {Lib }}} \quad\left\{\begin{array}{c}
\mathcal{P}_{\text {elec }} \quad \begin{array}{c}
\text { la puissance electrique de la station en } W \\
E_{\text {Lib }}: l^{\prime} \text { energie liberée par une fission d’un noyau en } J \\
N: \text { le nombre de noyaux d’uranium }-235 \text { consomé } \\
\text { pendant la durée } \Delta t \text { en sec }
\end{array}
\end{array}\right.
$$
2) la fusion nucléaire
La fusion nucléaire est une réaction nucléaire provoquée, au cours de laquelle deux noyaux légers s’associent pour former un noyau plus lourd
La réaction de fusion libère de l’énergie.
Exemple
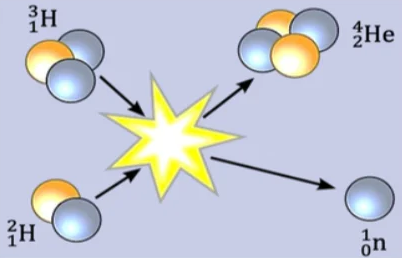
𓄲 l’énergie de la réaction
$$
{ }_1^2 \mathrm{H}+{ }_1^3 \mathrm{H} \rightarrow{ }_2^4 \mathrm{He}+{ }_0^1 n
$$
L’énergie libérée par la fusion d’un noyau ${ }_1^2 \mathrm{H}$ est un noyau ${ }_1^3 \mathrm{H}$ est :
$$
E_{\text {Lib }}=\left|m(H e)+m(n)-m\left({ }^2 H\right)-m\left({ }^3 H\right)\right| \cdot C^2=\left|E_L\left({ }_1^2 H\right)-E_L\left({ }_1^3 H\right)-E_L\left({ }_2^4 H e\right)\right|
$$
La fusion de deux noyaux ne se produit que si l’énergie cinétique des noyaux est suffisante pour échapper aux interactions répulsives.
3) La courbe d’Aston
⊹ \& Pour $A<40$, on constante que $\left(-\xi_L\right)$ augmente rapidement. il correspond aux petits noyaux instables ce qui pousse ces noyaux à s’associer entre eux pour former d’autres noyaux plus lourds et plus stables. Ce phénomènes est appelé Fusion nucléaire.
⊹ \& Pour $A>190$, on constate que ( $-\xi_L$ ) augmente lentement. Les noyaux correspondants sont instables ce qui les poussent à se dissocier pour former d’autres noyaux plus légers plus stable. Ce phénomènes est appelé fission nucléaire.
Parmi les isotopes du rubidium, on distingue le rubidium $85\left({ }_{37}^{85} R b\right)$ et le rubidium $89\left({ }_{37}^{89} R b\right)$.
1. Calculer l’énergies de liaison pour chaque noyau de ces deux isotopes.
2. En déduire l’énergie de liaison par nucléon pour chacun de ces deux isotopes.
3. Lequel de ces deux isotopes du rubidium est le plus stable ?
Données : $\quad 1 \mathrm{u}=931,5 \mathrm{MeV} . \mathrm{c}^{-2}$
$$
\begin{array}{|c|c|c|c|c|}
\hline \text { La particule } & { }_{37}^{85} R b & { }_{37}^{89} R b & \text { proton } & \text { neutron } \\
\hline \text { La masse en u } & 84,89144 \mathrm{u} & 88,89193 \mathrm{u} & 1,0073 \mathrm{u} & 1,0086 \mathrm{u} \\
\hline
\end{array}
$$
On considère les deux réactions nucléaires suivantes :
$$
{ }_0^1 n+{ }_{92}^{235} U \rightarrow{ }_{38}^{94} S r+{ }_Z^{140} \mathrm{Xe} e+y_0^1 n
$$
$$
{ }_1^2 H+{ }_1^3 H \rightarrow{ }_2^4 H e+{ }_b^a x
$$
1. Justifier que la réaction (1) est une fission alors que la réaction (2) est une fusion.
2. On s’intéresse à la réaction nucléaire (1):
a. Déterminer les valeurs de $Z$ et de $y$ en précisant les lois utilisées.
b. Calculer l’énergie Elibérée par cette réaction.
c. En déduire l’énergie $\mathrm{E}_1^{\prime}$ (en MeV ) libérée par la fission de 5 g d’uranium 235.
3. On s’intéresse à la réaction nucléaire (2) :
a. Montrer que la particule ${ }_b^a x$ émise au cours de cette réaction est un neutron.
b. Calculer l’énergie $E_2$ libérée par cette réaction.
c. En déduire l’énergie $\mathrm{E}_2$ libérée par la fusion lors de la formation 5 g d’hélium.
4. Comparer les énergies dégagées par les réactions de fusion et fission nucléaires. Conclure. On donne :
$$
\begin{array}{|l|c|c|c|c|c|c|c|}
\hline \text { Particule } & { }_{92}^{235} \mathrm{U} & { }_{38}^{94} \mathrm{Sr} & { }_Z^{140} \mathrm{Xe} & { }_1^2 \mathrm{H} & { }_1^3 \mathrm{H} & { }_2^4 \mathrm{He} & { }_0^1 n \\
\hline \text { La masse u } & 234,99332 & 93,89446 & 139,89195 & 2,01355 & 3,01550 & 4,00150 & 1,00867 \\
\hline
\end{array}
$$
$$
1 u=1,66.10^{-27} \mathrm{Kg}=931,5 \mathrm{MeV} . \mathrm{c}^{-2} .
$$
En 1934, Iréne et Frédéric Curie ont découvert la radioactivité artificielle en bombardant des noyaux d’aluminium 27 par des particules $\alpha\left({ }^4 \mathrm{He}\right.$ ). Il se forme alors du phosphore radioactif ${ }_{15}^{30} P$ selon l’équation : ${ }_{13}^{27} \mathrm{Al}+{ }_2^4 \mathrm{He} \rightarrow{ }_{15}^{30} \mathrm{P}+{ }_2^A x$.
1) a) Identifier la particule $\times$ émise. Tout en prédisant les lois de conservation utilisées.
b) S’agit-il d’une réaction spontanée ou provoquée ?
c) calculer l’énergie de cette réaction. Conclure.
2) Le phosphore ${ }_{15}^{30} P$ se désintègre à son tour en silicium $S i$ avec émission d’une particule $\boldsymbol{\beta}^{+}$selon l’équation
$$
{ }_{15}^{30} P \longrightarrow{ }_{14}^{30} S i+{ }_1^0 e
$$
En se référant aux nombres de neutrons et de protons des noyaux de phosphore et de silicium, montrer que la particule $\beta^{+}$résulte de la transformation dans le noyau d’un proton en in neutron.
3) sachant que le défaut de masse du noyau ${ }_{15}^{30} P$ est $\Delta m=0,2617 \mathrm{u}$ et que l’énergie de liaison du noyau ${ }_{14}^{30} S i$ est $\mathrm{E}_{\mathrm{L}}=248,91 \mathrm{Mev}$ :
a) Calculer en Mev, l’énergie de liaison du noyau ${ }_{15}^{30} P$.
b) Comparer les stabilités des noyaux ${ }_{15}^{30} \mathrm{P}$ et ${ }_{14}^{30} \mathrm{Si}$.
On donne : $\quad 1 \mathrm{u}=931,5 \mathrm{Mev} . \mathrm{C}^{-2}$, et les masses atomiques :
$$
\begin{array}{|c|c|c|c|c|}
\hline \text { Particule } & { }_2^4 \mathrm{He} & { }_Z^4 \boldsymbol{x} & { }_{13}^{27} \mathrm{Al} & { }_{15}^{30} P \\
\hline \text { Masse en u } & 4,0015 & 1,0086 & 26,9815 & 29,9783 \\
\hline
\end{array}
$$