Ondes mécaniques progressives périodiques
I. Définition
Une onde progressive est dite périodique si l’évolution temporelle de chaque point du milieu de propagation est périodique.
II. La double périodicité temporelle et spatiale
L’onde mécanique progressive périodique se caractérise par :
✹ La période temporelle notée $T$, c’est la durée minimale nécessaire pour qu’un point du milieu retrouve le même état de vibration.
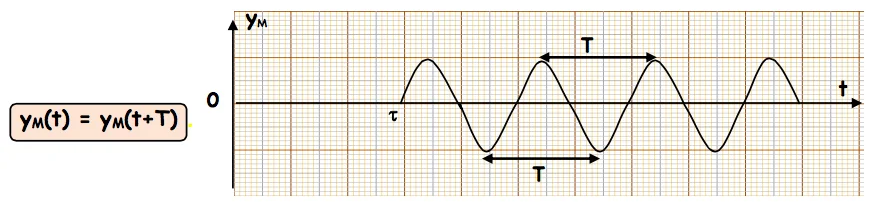
La fréquence est le nombre de périodes par sec $N=1 / T$
✹ La période spatiale notée $\lambda$, appelée aussi longueur d’onde, c’est la distance minimale entre deux points qui ont la même élongation à chaque instant.
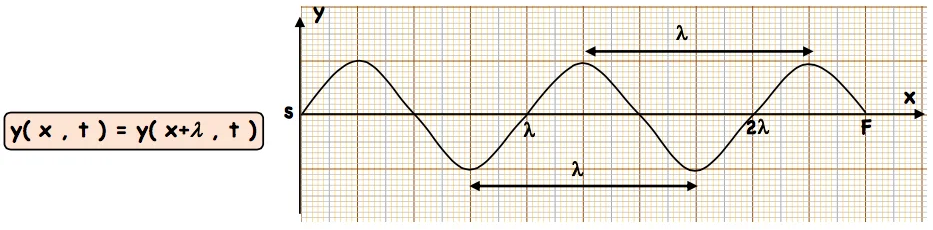
Remarque
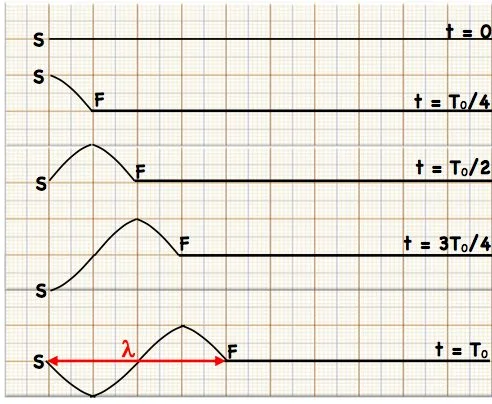
distance parcouru par l’onde pendant une période temporelle
La longueur d’onde est la
Donc
$$
v=\frac{\lambda}{T}=\lambda . N
$$
III. la comparaison du mouvement de deux points
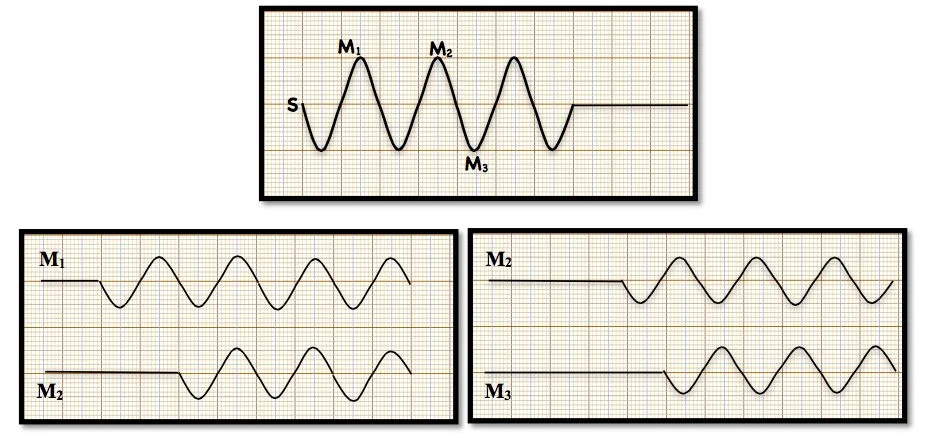
✹ $M_1 M_2=\lambda$ et $y_1(t)=y_2(t)$. On dit que $M_1$ et $M_2$ vibrent en phase
✹ $M_2 M_3=0,5$. $\lambda$ et $y_2(t)=-y_3(t)$. On dit que $M_2$ et $M_3$ vibrent en opposition de phase Le cas générale :
✹ $M_1 M_2=S M_2-S M_1=k . \lambda \quad\left(k \in \mathbb{Z}^*\right)$ on a $y_1(t)=y_2(t)$ et les deux points vibrent en phase \& $M_2 M_3=S M_2-S M_1\left(k+\frac{1}{2}\right) \cdot \lambda \quad(k \in \mathbb{Z})$ on $a y_1(t)=-y_2(t)$ et les deux points vibrent en opposition de phase.
Remarque :
La longueur d’onde est la distance entre deux point successif en phase.
VI. Étude expérimental
1) Détermination de la vitesse des ondes sonores
Pour déterminer la vitesse de propagation du son émis par un haut-parleur dans l’air on utilise le montage suivant:
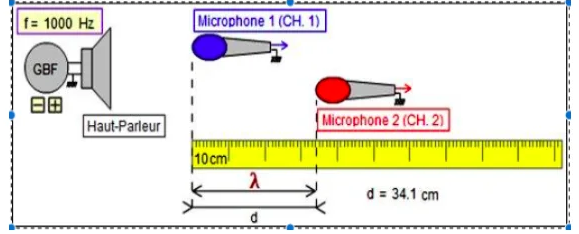
Après avoir activé le haut-parleur on visualise sur l’écran de l’oscilloscope le signal correspondant à chacun des microphones $M_1$ et $M_2$. Lorsque les deux microphones sont placés côte à côte face au haut-parleur et à la même distance de lui, les deux signaux correspondant à $M_1$ et à $M_2$ sont en phase.
Pour un son émis de fréquence de $N$, on laisse le microphone $M_1$ à sa place et on déplace le microphone $M_2$ lentement et parallèlement à l’axe du haut-parleur.
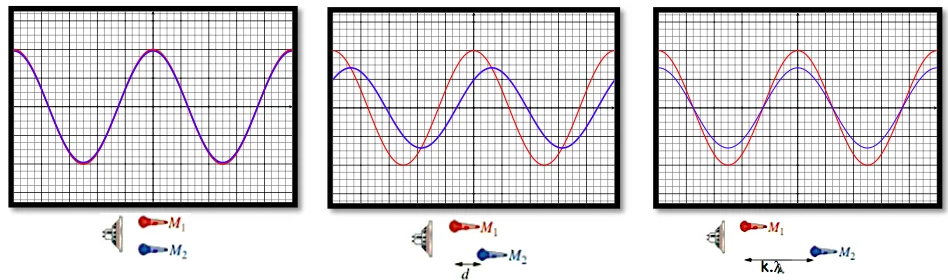
On indique la distance $d$ chaque fois que les deux signaux sont en phase et on obtient les résultats suivants:
$$
\begin{array}{|c|c|c|c|c|}
\hline K & 1 & 2 & 3 & 4 \\
\hline d(c m) & 34 & 68 & 102 & 136 \\
\hline
\end{array}
$$
• $\lambda=34 \mathrm{~cm}$ ( la plus petite distance entre deux point en phase )
• la fréquence $N=\frac{1}{T}=\frac{1}{5.0,2.10^{-3}}$ donc $N=1 \mathrm{kHz}$.
• la vitesse $v=\lambda . N=340 \mathrm{~m} / \mathrm{s}$.
2) la vitesse de propagation des ondes à la surface de l’eau (étude stroboscopique)
Le stroboscope est un dispositif électronique qui émet des flashs périodiques.
Soit $T_s$ la période des éclairs et $T$ la période de rotation d’un disque contenant une tache
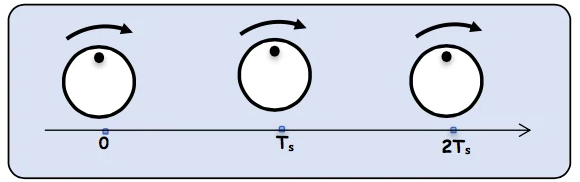
Pour que le disque apparaît immobile, il faut qu’il fasse $\mathbf{k}$ tour complet entre deux éclaires donc: $\quad T_S=k T$ ou $N=k N_S \quad$ pour $k=1$ on à $\quad N=N_{S_{\max }}$
On éclaire avec un stroboscope la surface de l’eau dans une cuve à onde où on craie une perturbation périodique
On observe des zones brillantes qui corresponds aux points d’élongation maximum et des zones sombres qui correspond aux points d’élongation minimum.
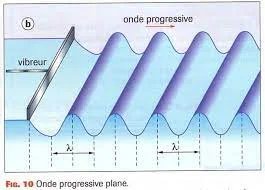

la longueur d’onde est la distance entre deux franges consécutive de même nature : $V=\lambda$.
V. La diffraction des ondes
1) Définition
La diffraction est une déformation subit par l’onde lorsqu’elle rencontre une ouverture ou un obstacle.

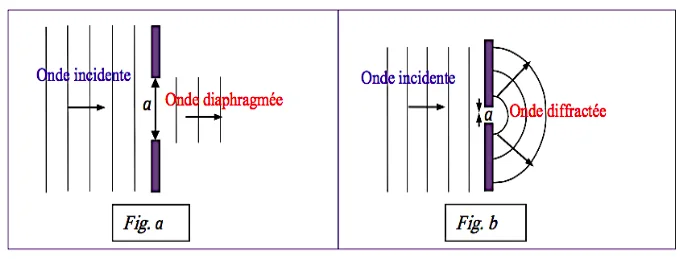
2) condition d’observation
✹ Pour avoir le phénomène de diffraction il faut que la largeur de la fente soit inférieur ou égal à
la longueur d’onde.
✹ L’onde diffractée et l’onde incidente ont la même fréquence, même célérité et, par conséquence, même longueur d’onde.
✹ Le phénomène de diffraction montre la nature ondulatoire de toute perturbation qui se propage.
IV. Les milieux dispersifs.
1) étude expérimentale
On craie des ondes circulaires à la surface de l’eau par une source ponctuelle de fréquence réglable.
On fait varier la fréquence $\mathbf{N}$ et on note la valeur de $\lambda$ puits on calcule la valeur de la célérité on obtient les résultats suivants.
$$
\begin{array}{|c|c|c|c|c|c|c|}
\hline \text { Fen Hz } & 15,1 & 20,0 & 25,2 & 30,6 & 39,4 & 60,1 \\
\hline \lambda \text { en m } & 1,46 \cdot 10^{-2} & 1,13 \cdot 10^{-2} & 9,33 \cdot 10^{-3} & 8,98 \cdot 10^{-3} & 7,77 \cdot 10^{-3} & 5,68 \cdot 10^{-3} \\
\hline \text { Ven m/s } & 0,220 & 0,225 & 0,235 & 0,275 & 0,306 & 0,341 \\
\hline
\end{array}
$$
On constate que la vitesse de propagation de l’onde n’est pas constant, elle dépend de la fréquence.
2) les milieux dispersifs
On appelle milieu dispersif, un milieu matériel dans lequel la célérité des ondes sinusoïdales dépend de leur fréquence.
Exercice
Recopier le numéro de la question et écrire à côté, parmi les quatre réponses proposées, la réponse juste sans aucune justification ni explication.
– Propagation d’une onde mécanique à la surface de l’eau :
On crée, à l’instant $t=0$, en un point $S$ de la surface de l’eau, une onde mécanique progressive sinusoïdale de fréquence $N=50 \mathrm{~Hz}$.
La figure ci-dessous représente une coupe verticale de la surface de l’eau à un instant $t$.
La règle graduée sur le schéma indique l’échelle utilisée.

1- La longueur d’onde est :
$$
\boxminus \lambda=0,2 \mathrm{~cm} \quad \boxminus \lambda=4 \mathrm{~cm} \quad \boxminus \lambda=5 \mathrm{~cm} \quad \boxminus \lambda=6 \mathrm{~cm}
$$
2- La vitesse de propagation de l’onde à la surface de l’eau est :
☐ $\mathrm{v}=2 \mathrm{~m} \cdot \mathrm{~s}^{-1}$
☐$\mathrm{v}=200 \mathrm{~m} \cdot \mathrm{~s}^{-1}$
☐ $\mathrm{v}=3 \mathrm{~m} . \mathrm{s}^{-1}$
☐$$
\square v=8.10^{-4} \mathrm{~m} \cdot \mathrm{~s}^{-1}
$$
3- L’instant $t$, où la coupe de la surface de l’eau est représentée, a pour valeur :
☐$\square t=8 s$
☐$t=0,03 s$
☐$\square t=0,3 s$
☐$t=3 s$
4- On considère un point $M$ de la surface de l’eau, éloigné de la source $S$ d’une distance $S M=6 \mathrm{~cm}$.
Le point $M$ reprend le même mouvement que celui de $S$ avec un retard temporel $\tau$.
la relation entre l’élongation du point $M$ et celle de la source $S$ s’écrit :
$\begin{array}{ll}\square y_M(t)=y_S(t-0,3) & \square y_M(t)=y_S(t+0,03) \\ \square y_M(t)=y_S(t-0,03) & \square y_M(t)=y_S(t+0,3)\end{array}$