Ondes mécaniques progressives
I. Onde mécanique et vitesse de propagation
1) Onde mécanique.
On appelle onde mécanique le phénomène de propagation d’une perturbation dans un milieu élastique. Cette propagation se fait avec transport d’énergie et sans transport de matière.
2) propriétés d’une onde
➤ Onde unidimensionnel qui se propage dans une seul direction (la corde et le ressort)
➤ Onde bidimensionnel qui se propage dans un plan (la surface de l’eau)
➤ Onde tridimensionnel se propage dans l’espace (le son)
3) Types d’ondes mécaniques
✹ Une onde transversale provoque une perturbation dont la direction est perpendiculaire à la direction de propagation de l’onde.
Par exemple: une onde à la surface de l’eau, onde le long d’une corde.
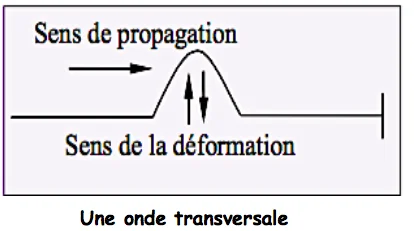
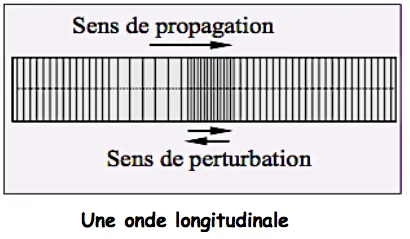
✹ Une onde longitudinale est une perturbation dont la direction est parallèle à la direction de propagation de l’onde.
Par exemple un ressort, le son …
4) La vitesse de propagation (la célérité)
Les ondes se propagent dans les milieux homogènes avec une vitesse constante, elle dépend des propriétés du milieu (l’élasticité et l’inertie) et s’exprime par le rapport de la distance d parcourue par l’onde pendant une durée :
$$
V=d / \Delta t
$$
Exemple:
⊹ La vitesse d’une onde se déplaçant le long d’une corde dépend de la masse linéique de la corde et de sa tension $V=\sqrt{\frac{F}{\mu}} \mu=m / L$ et la masse linéique de la corde.
⊹ La vitesse d’une onde se propageant a la surface de l’eau dépend de la profondeur $h$ de l’eau $\quad V=\sqrt{g . h} \quad g$ et le champ de pesanteur.
⊹ La vitesse d’une onde sonore dans un gaz $V=\sqrt{\frac{\gamma \mathbf{P}}{\rho}}=\sqrt{\frac{\gamma \mathbf{R T}}{M}} \quad \gamma$ est une constante sans unité qui caractérise le gaz.
Remarque :
Pour l’onde sonore, la célérité augmente avec la densité du milieu de propagation. $\mathbf{v}_{\text {gaz }}<\mathbf{V}_{\text {liquide }}<\mathbf{v}_{\text {solide }}$
II. Onde mécanique progressive
1) Définition
C’est la propagation d’un mouvement vibratoire entretenu dans un milieu matériel élastique supposé infini.
2) le retard temporel
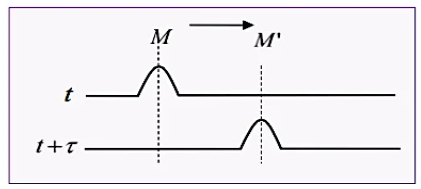
le retard temporel d’un point $M$ par rapport à la source $M^{\prime}$ est le temps nécessaire à l’onde pour traverser la distance MM’, on le note $\tau$.
$\tau=M M^{\prime} / V$
3) L’élongation d’un point M
L’élongation d’un point est la distance d’évolution de ce point autour de sa position d’équilibre on la note $y$.
$y$ est une valeur algébrique, sa valeur maximum s’appelle amplitude.
Remarques:
✹ L’élongation dépond du temps et de la position par rapport à la source $S$ donc
$$
y=f(x, t) \quad \text { avec } x=S M
$$
✹ Chaque point refait le même mouvement de la source $S$ mais après un retard $\tau$
$$
y_M(t)=y_s(t-\tau)
$$
✹ À un instant $t_1$ donné, $y=f(x)$ présente l’aspect (l’image) de l’onde
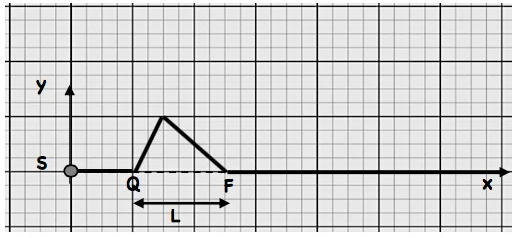
L’aspect de l’onde à l’instant $t_1$
F: le front d’onde $\quad$; $Q$ : la queue de l’onde $: \quad L=Q F$ La longueur de l’onde
✹ Pour un point $M_1\left(x_1=c t e\right), y_{M_1}=f(t)$ présente la variation de l’élongation de $M_1$ en fonction du temps.
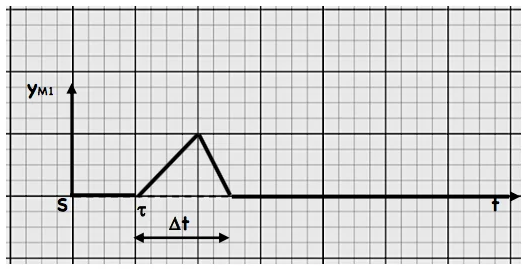
L’élongation d’un point $M_1$
$\tau$ : Le retard temporel
$\Delta t$ : la durée de l’onde
On a $\quad V=L / \Delta t$
– Exercice 1
Célérité du son dans l’acier: Sur un chantier, un ouvrier frappe un coup à l’extrémité d’une tige en acier de 100 m de long. Un second ouvrier, situé à l’autre extrémité de la poutre, entend alors 2 coup successifs. La célérité du son dans l’air est de $340 \mathrm{~m} / \mathrm{s}$.
– Expliquer pourquoi l’ouvrier entend deux coups.
– Sachant que la durée qui sépare les deux coups est de $0,277 \mathrm{~s}$, calculer la célérité de l’onde dans l’acier de la tige.
– Exercice 2
Détection sous-marine: Une explosion a lieu 50 m au-dessus de la surface de la mer. La vitesse du son est d’environ $340 \mathrm{~m} / \mathrm{s}$ dans l’air et de $1500 \mathrm{~m} / \mathrm{s}$ dans l’eau. Au bout de combien de temps, un sous-marin situé exactement sous le point d’explosion à 30 m de profondeur, détecte-t-il le bruit d’explosion ?
Exercice 3
La figure ci-dessous représente l’aspect d’une corde tendue à deux instants différents $\boldsymbol{t}_1=0,6 \mathrm{~s}$ et $t_2=1,4 \mathrm{~s}$.
1- Calculer la célérité de l’onde le long de la corde.
2- Déduire la durée de déformation.
3- À quel instant la perturbation a- t-elle commencé sa propagation à partir de la source ?
4- Représenter l’aspect de la corde à l’instant $t_3=1,28 \mathrm{~s}$.
– Exercice 4
On crée par vibreur à l’instant t=0 une déformation à l’extrémité $S$ d’une corde élastique. la figure ci-dessous représente l’allure de la corde à l’instant $t_1=60 \mathrm{~ms}$.
1-Quelle est la nature de cette onde ? (longitudinale ou transversale).
2-Cette onde est-elle unidimensionnelle; bidimensionnelle ou tridimensionnelle ?
3-Calculer la célérité de propagation le long de la corde. Quelle est la longueur de la perturbation ? Quelle est sa durée ?
4-Déterminer à l’instant $t_1$ les points qui effectuent un mouvement vers le haut et les points qui effectuent un mouvement vers le bas.
5-Représenter l’allure de la corde à l’instant $t_2=90 \mathrm{~ms}$.
7-Determiner le retard temporel entre le point $M_4$ et $S$
8-Ecrire l’élongation du point $M_4$ en fonction de celle de la source $S$.