Les réactions acide – base
I. Les solutions aqueuses
1) Autoprotolyse de l’eau.
L’autoprotolyse de l’eau est la réaction qui se produit entre les molécules $\mathrm{H}_2 \mathrm{O}$ appartenant aux couples $\mathrm{H}_2 \mathrm{O} / \mathrm{HO}^{-}$et $\mathrm{H}_3 \mathrm{O}^{+} / \mathrm{H}_2 \mathrm{O}$.
$$
2 \mathrm{H}_2 \mathrm{O} \leftrightarrows \mathrm{H}_3 \mathrm{O}++\mathrm{HO}^{-}
$$
2) Le produit ionique de l’eau.
Le produit ionique de l’eau est la constante d’équilibre de la réaction d’autoprotolyse de l’eau. On la note Ke .
$$
\mathrm{K}_{\mathrm{e}}=\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_{\mathrm{eq}} \cdot\left[\mathrm{HO}^{-}\right]_{\mathrm{eq}}
$$
Ke est une grandeur sans unité alors que les concentrations sont en mol/L.
Remarques :
• Ke est constante dans toutes les solutions aqueuses quel que soit leurs natures et ne dépend que de la température (Ke croit lorsque la température augmente).
• pKe est une constante telle que pKe $=-\log (\mathrm{Ke})$ ou $\mathrm{Ke}=10^{-\mathrm{pKe}}$.
$$
\begin{array}{|c|c|c|}
\hline \text { température }{ }^{\circ} \mathrm{C} & \text { Ke }\left(\text { en } 10^{-14}\right) & \text { pKe } \\
\hline 0 & 0,12 & 14,9 \\
\hline 18 & 0,58 & 14,23 \\
\hline 25 & 1 & 14,00 \\
\hline 50 & 5,6 & 13,25 \\
\hline 75 & 19 & 12,72 \\
\hline 100 & 48 & 12,32 \\
\hline
\end{array}
$$
• $$
\text { – PH }=-\log \left[\mathrm{H}_3 \mathrm{O}^{+}\right]_{\text {eq }} \Rightarrow \mathrm{PH}=-\log \left(\mathrm{Ke} /\left[\mathrm{HO}^{-}\right]_{\mathrm{eq}}\right) \Rightarrow \mathrm{PH}=\mathrm{PKe}+\log \left(\left[\mathrm{HO}^{-}\right]_{\text {eq }}\right) \text {. }
$$
3) Échelle de pH.
Le pH des solutions aqueuses usuelles s’étend de O à pKe. La nature acide, basique ou neutre d’une solution dépend de son pH
* Une solution est acide si $\left.\left.\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\right\rangle\left[\mathrm{HO}^{-}\right] \Leftrightarrow\left[\mathrm{H}_3 \mathrm{O}^{+}\right]^2\right\rangle \mathrm{Ke} \quad \Leftrightarrow \mathrm{PH}\left\langle\frac{1}{2} \mathrm{PKe}\right.$
* Une solution est basique si $\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left\langle\left[\mathrm{HO}^{-}\right] \Leftrightarrow\left[\mathrm{H}_3 \mathrm{O}^{+}\right]^2\langle\mathrm{Ke} \Leftrightarrow \mathrm{PH}\rangle \frac{1}{2} \mathrm{PKe}\right.$
Une solution est neutre si $\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\left[\mathrm{HO}^{-}\right] \Leftrightarrow\left[\mathrm{H}_3 \mathrm{O}^{+}\right]^2=\mathrm{Ke} \Leftrightarrow \mathrm{PH}=\frac{1}{2} \mathrm{PKe}$

II. la constante d'acidité d'un couple acide-base.
1) Définition
La constante d’acidité $K_a$ d’un couple acide-base est la constante d’équilibre de la réaction de l’acide sur l’eau.
2) L’expression
On considère le couple $A H / A^{-}$, on a $A H_{a q}+H_2 \mathrm{O}_{\mathrm{L}} \leftrightarrows{A^{-}}^{-q}+\mathrm{H}_3 \mathrm{O}^{+}$aq On a $\mathrm{K}_{\mathrm{A}}=\frac{\left[A^{-}\right] \cdot\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{[A H]}$
3) propriétés
– K $K_A$ est une constante qui caractérise le couple $A H / A^{-}$dans toutes les solutions aqueuses, et ne dépend que de la température.
– $K_A$ est sans unité avec des concentrations en mol/L.
– pK_ est une constante telle que $p K_A=-\log \left(K_A\right)$ ou $K_A=10^{-p K A}$.
4) exemples.
À $25^{\circ} \mathrm{C}$ :
✹ $\mathrm{H}_3 \mathrm{O}^{+} / \mathrm{H}_2 \mathrm{O}, \mathrm{K}_{\mathrm{A}}=1 .\left[\mathrm{H}_3 \mathrm{O}^{+}\right] /\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=1$ donc $\mathrm{pk}_{\mathrm{A}}=0$.
✹ \& $\mathrm{H}_2 \mathrm{O} / \mathrm{HO}^{-}, \mathrm{K}_{\mathrm{A}}=\left[\mathrm{HO}^{-}\right] \cdot\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\mathrm{Ke}$ donc $\mathrm{pk}_{\mathrm{A}}=\mathrm{pke}=14$.
✹ \& $\mathrm{CH}_3 \mathrm{COOH} / \mathrm{CH}_3 \mathrm{COO}^{-}, \mathrm{K}_{\mathrm{A}}=\frac{\left[\mathrm{CH}_3 \mathrm{CO}_2^{-}\right] \cdot\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{\left[\mathrm{CH}_3 \mathrm{CO}_2 \mathrm{H}\right]}=1,6 \cdot 10^{-5}$ donc $\mathrm{pK}_{\mathrm{A}}=4,8$
5) La constante d’équilibre d’une réaction acide base
On considère deux couples acide-base $A_1 H / A_1{ }^{-}$et $A_2 H / A_2$ – de constante d’acidité respectivement $K_{A 1}$ et $K_{A 2}$.
Soit la réaction modélisée par l’équation suivante : $A_1 H_{a q}+A_2{ }^{-}{ }_{\text {aq }} \leftrightarrows A_1{ }^{-}{ }_{\text {aq }}+A_2 H_{a q}$ la constante d’équilibre de cette réaction est $K=\frac{\left[A_1^{-}\right] \cdot\left[A_2 H\right]}{\left[A_1 H\right] \cdot\left[A_2^{-}\right]}$.
$$
\Leftrightarrow \quad K=\frac{\left[A_1^{-}\right] \cdot\left[H_3 O^{+}\right] \cdot\left[A_2 H\right]}{\left[A_1 H\right] \cdot\left[A_2^{-}\right] \cdot\left[H_3 O^{+}\right]} \quad \Leftrightarrow \quad K=\frac{K_{A 1}}{K_{A 2}}=\frac{10^{-P K A 1}}{10^{-P K A 2}}=10^{\left(P K_{A 2}-P K_{A 1}\right)}
$$
$$
\Leftrightarrow \quad K=10^{\left(P K_{A 2}-P K_{A 1}\right)}=10^{\triangle P K_A}
$$
III. la comparaison de la réactivité des acides et des bases
1) La réactivité des acides.
$$
\mathrm{AH}+\mathrm{H}_2 \mathrm{O} \leftrightarrows \mathrm{~A}^{-}+\mathrm{H}_3 \mathrm{O}^{+} \quad \text { on } a \mathrm{~K}_{\mathrm{A}}=\frac{\left[\mathrm{A}^{-}\right] .\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{[\mathrm{AH}]}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]^2}{\mathrm{C}-\left[\mathrm{H}_3 \mathrm{O}^{+}\right]} \text {et }\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\mathrm{C} . \tau
$$
Donc $K_A=\frac{C . \tau^2}{1-\tau}$
On considère deux acide $A_1 H$ et $A_2 H$ de même concentration, l’acide $A_1 H$ est plus réactif que $A_2 H$
$$
\text { si } \left.\left.\tau_1\right\rangle \tau_2 \Leftrightarrow \mathrm{~K}_{\mathrm{A} 1}\right\rangle \mathrm{K}_{\mathrm{A} 2} \Leftrightarrow \mathrm{PK}_{\mathrm{A} 1}\left\langle\mathrm{PK} \mathrm{~A}_{\mathrm{A} 2}\right.
$$
L’acide est d’autant plus réactif que le $\mathrm{pK}_{\mathrm{A}}$ de son couple est faible
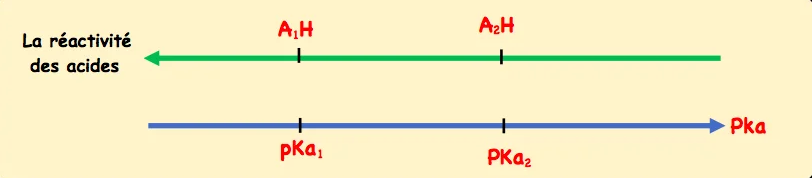
2) la réactivité des bases.
$$
\begin{aligned}
& \mathrm{A}^{-}+\mathrm{H}_2 \mathrm{O} \leftrightarrows \mathrm{AH}+\mathrm{HO}^{-} \text {on a } \mathrm{K}_{\mathrm{A}}=\frac{\left[\mathrm{A}^{-}\right] \cdot\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{[\mathrm{AH}]}=\frac{c-\left[\mathrm{HO}^{-}\right]}{\left[\mathrm{HO}^{-}\right]^2} \mathrm{Ke} \text { et }\left[\mathrm{HO}^{-}\right]=\mathrm{C} \cdot \tau \\
& \text { donc } \mathrm{K}_{\mathrm{A}}=\mathrm{Ke} \cdot \frac{1-\tau}{\mathrm{C} \cdot \tau^2}
\end{aligned}
$$
On considère deux base $A_1^{-}$et $A_2^{-}$de même concentration, la base $A_2^{-}$est plus réactif que $A_1^{-}$si
$$
\left.\tau_2\right\rangle \tau_1 \Leftrightarrow \mathrm{~K}_{\mathrm{A} 2}\left\langle\mathrm{~K}_{\mathrm{A} 1} \Leftrightarrow \mathrm{P} K_{A 2}\right\rangle P K_{A 1} .
$$
La base est d’autant plus réactif que le $p K_A$ de son couple est grand.
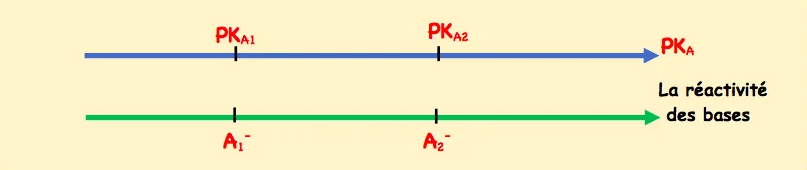
Conclusion
Soient deux couples acide-base $\mathrm{A}_1 \mathrm{H} / \mathrm{A}_1^{-}$et $\mathrm{A}_2 \mathrm{H} / \mathrm{A}_2^{-}$de constante d’acidité $\mathrm{pK} \mathrm{Al}_{\mathrm{Al}}$ et $\mathrm{pK} \mathrm{A}_{\mathrm{A} 2}$.
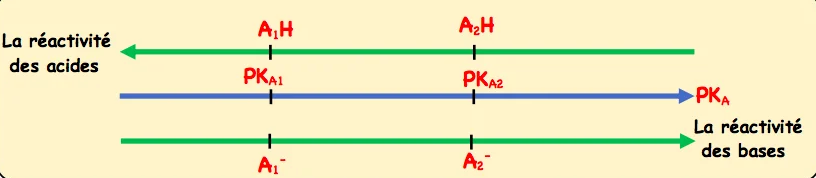
Exemple
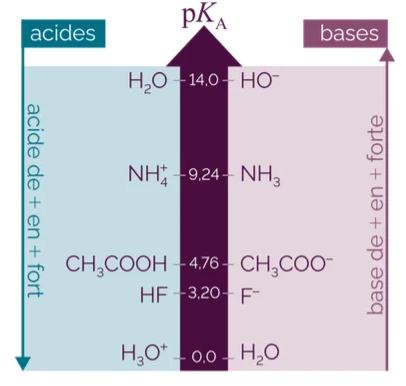
IV. domaine de prédominance
1) PH en fonction de pKa
Pour un couple $\mathrm{AH} / \mathrm{A}^{-}$on a $\mathrm{K}_{\mathrm{A}}=\frac{\left[\mathrm{A}^{-}\right] \cdot\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{[\mathrm{AH}]}$ donc $\mathrm{PK} \mathrm{K}_{\mathrm{A}}=\mathrm{PH}-\log \left(\frac{\left[A^{-}\right]}{[A H]}\right)$
d’où
$$
\mathrm{PH}=\mathrm{PK}_{\mathrm{A}}+\log \left(\frac{\left[A^{-}\right]}{[A H]}\right)
$$
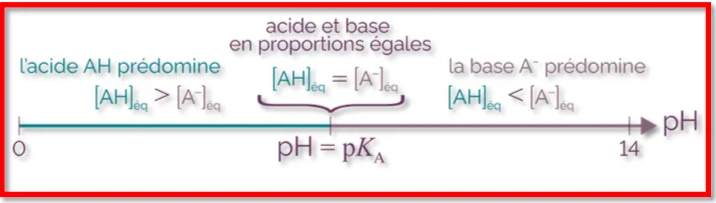
2) Domaine de prédominance acide base
⊹ L’acide AH est prédominant si $[A H]\rangle\left[A^{-}\right] \Leftrightarrow P H\left\langle\mathrm{PK}_{\mathrm{A}}\right.$
⊹ La base $A^{-e s t}$ prédominante si $\left.\left[A^{-}\right]\right\rangle[A H] \Leftrightarrow P H>\mathrm{PK}_A$
⊹ Pour $[\mathbf{A H}]=\left[\boldsymbol{A}^{-}\right]$on a $\mathrm{PH}=\mathrm{PK}_{\mathrm{A}}$
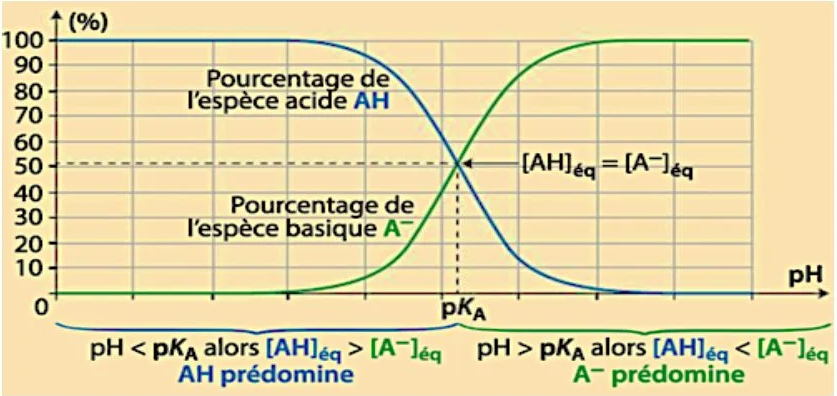
3) Diagramme de distribution
Le diagramme de distribution d’un couple acide-base est la représentation de la répartition de l’acide et de la base en fonction du pH de la solution.
4) Les indicateurs colorés
Un indicateur coloré est un couple acide/base (on le notera: HInd/Ind-), dont la forme acide HInd et la forme basique Ind ont des couleurs différentes en solution.
Ce couple est caractérisé par la constante d’acidité Ki . donc
$$
\mathrm{PH}=\mathrm{PK}_{\mathrm{i}}+\log \left(\left[\text { Ind }^{-}\right] /[\mathrm{HInd}]\right)
$$
✹ La solution dans laquelle se trouve l’indicateur a la couleur de la forme acide InH si
$$
\text { [HInd] }\rangle 10 .\left[\text { Ind }^{-}\right] \Leftrightarrow \mathrm{PH}\left\langle\mathrm{PK}_{\mathrm{i}}-1 .\right.
$$
✹ La solution dans laquelle se trouve l’indicateur a la couleur de la forme base Ind’ si
$$
\text { [Ind } \left.\left.{ }^{-}\right]\right\rangle 10 .[H I n d] \Leftrightarrow \mathrm{PH}>\mathrm{PK}_{\mathrm{i}}+1
$$
✹ La solution prendra une couleur appelée teinte sensible (mélange des couleurs dues à la forme acide et à la forme basique) si : [HInd] et [Ind-] sont du même ordre de grandeur dans ce cas $\mathrm{PK}_{\mathrm{i}}-1<\mathrm{PH}\left\langle\mathrm{PK}_{\mathrm{i}}+1\right.$. Cette zone s’appelle zone de virage.

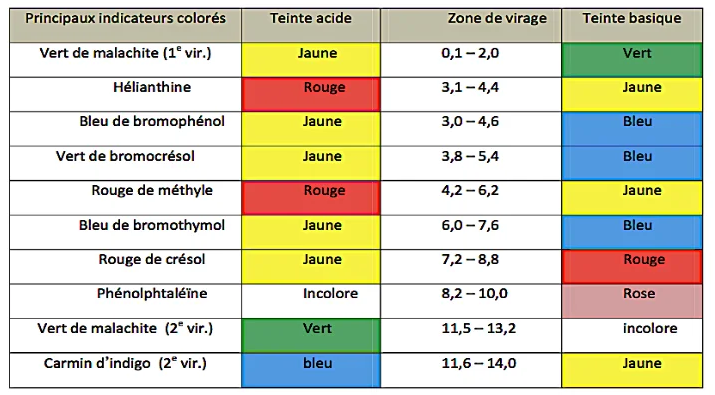
– Exemples
Zone de virage des principaux indicateurs colorés
Exercice 1
1) $\AA \grave{1} 10^{\circ} \mathrm{c}$ l’eau pure a un $\mathrm{PH}=7,27$.
Calculer la valeur de PH d’une solution aqueuse à $10^{\circ} \mathrm{C}$ dont la concentration en ion hydroxyde est $\left[\mathrm{HO}^{-}\right]=10^{-5} \mathrm{~mol} / \mathrm{L}$.
2) $\AA ~ 60^{\circ} \mathrm{C}$ on $a \mathrm{Ke}=9,6 \cdot 10^{-14}$.
Quelle est la nature d’une solution de $\mathrm{PH}=6,8$ à $60^{\circ} \mathrm{C}$.
Exercice 2
On prépare un mélange ( S ) de volume V , en introduisant $n_1=2.10^{-3}$ mol d’acide éthanoïque et $n_2=10^{-3} \mathrm{~mol} d^{\prime} a m m o n i a c$, dans un récipient contenant de l’eau distillée. La transformation. ayant lieu, est modélisée par l’équation suivante : $\mathrm{CH}_3 \mathrm{COOH}+\mathrm{NH}_{3(a q)} \leftrightarrows \mathrm{CH}_3 \mathrm{COO}^{-}+\mathrm{NH}_4{ }^{+}$. On donne : $\mathrm{pK}_{\mathrm{A}}\left(\mathrm{CH}_3 \mathrm{COOH} / \mathrm{CH}_3 \mathrm{COO}\right): \mathrm{pK}_{\mathrm{Al}}=4,8 ; \mathrm{pK}_{\mathrm{A}}\left(\mathrm{NH}_4^{+} / \mathrm{NH}_3\right): \mathrm{pK}_{\mathrm{Al}}=9,2$.
1- Construire le tableau descriptif de l’évolution de cette réaction.
2- Établir l’expression du quotient de réaction à l’équilibre $Q_{r . e q}$ en fonction de $\mathrm{pK}_{\mathrm{Al}}$ et $\mathrm{pK}_{\mathrm{A} 2}$, puis calculer sa valeur.
3- Trouver le taux d’avancement final, et s’assurer que la transformation est totale.
4- Calculer le PH du mélange à l’état final et déduire les espèces prédominantes dans la solution.
1- Étude de la solution d’acide benzoïque
L’acide benzoïque est un solide blanc de formule $\mathrm{C}_6 \mathrm{H}_5 \mathrm{COOH}$, il est utilisé comme conservateur alimentaire et il est naturellement présent dans certaines plantes.
Pour simplifier, on symbolise l’acide benzoïque par $\mathrm{HA}_1$.
Données: Masse molaire moléculaire de l’acide $H A_1: M\left(H A_1\right)=122 \mathrm{~g} \cdot \mathrm{~mol}^{-1}$
Produit ionique de $\mathrm{l}^{\prime}$ eau à $25^{\circ} \mathrm{C}$ : $\mathrm{Ke}=10^{-14}$
On dissout une masse $\mathrm{m}=305 \mathrm{mg}$ de l’acide benzoïque dans de l’eau distillée pour obtenir une solution aqueuse $\mathrm{S}_{\mathrm{A}}$ de volume $\mathrm{V}=250 \mathrm{~mL}$.
La mesure du pH de la solution $\mathrm{S}_{\mathrm{A}}$ donne $\mathrm{pH}=3,10$.
1.1- Calculer la concentration molaire $C_A$ de la solution $S_A$.
1.2- Écrire l’équation de la réaction de l’acide benzoïque avec l’eau.
1.3- Exprimer la constante $\mathrm{PK}_A$ du couple $H A_1 / A_1^{-}$en fonction de $C_A$ et $\tau$, le taux d’avancement final de la réaction d’acide benzoïque avec l’eau.
1.4- Calculer le $\mathrm{pK}_{\mathrm{A}}$ et déduire l’espèce chimique prédominante dans la solution $\mathrm{S}_{\mathrm{A}}$ sachant que $\tau=7,94 \%$
2- Réaction entre une solution d’acide benzoïque et une solution d’hydroxyde de sodium On mélange un volume $V_A=40,0 \mathrm{~mL}$ de la solution $S_A$ de l’acide benzoïque avec un volume $V_B=5,00 \mathrm{~mL}$ d’une solution $\mathrm{S}_{\mathrm{B}}$ d’hydroxyde de sodium de concentration molaire $C_B=2,50.10^{-2}$ mol. $\mathrm{L}^{-1}$. La mesure du pH du mélange obtenu donne $\mathrm{pH}=3,80$.
2.1- Écrire l’équation de la réaction qui a lieu.
2.2- Calculer la quantité de matière $n\left(\mathrm{HO}^{-}\right)_{\mathrm{f}}$ qui se trouve dans le mélange à l’état final.
2.3- En déduire le taux d’avancement final de la réaction. On peut utiliser le tableau d’avancement du système (On néglige les ions $\mathrm{HO}^{-}$provenant de l’eau).
2.4- Calculer la valeur du pH du mélange à l’état d’équilibre.