Le circuit RC
I. Le condensateur.
1. Définition et symbole.
Un condensateur est constitué de deux plaques métalliques (les armatures) parallèles, séparés par un isolant (un diélectrique), son symbole est: 
Chacune de ces armatures porte une charge électrique, $q$ et $-q$ avec q > O la charge du condensateur.
La convention “récepteur” : la flèche représentant la tension u du dipôle est opposée à l’orientation du courant.
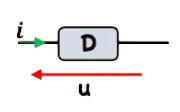
• Si D est un récepteur $u>0$ et $i>0 \quad(u \times i>0)$
Dipôle ohmique 
$$
u_{\mathrm{R}}=\mathrm{R} \times i
$$
• Si $D$ est un générateur $u\rangle 0$ et $i\langle 0$ ou $u\langle 0$ et $i\rangle 0(u \times i\langle 0)$
Générateur de tension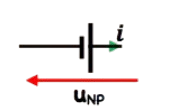 
$$
u_{N P}=-E+r i
$$
La convention “générateur” : la flèche représentant la tension $u$ du dipôle a le même sens que le courant.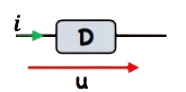
• Si D est un récepteur $u\rangle 0$ et $i\langle 0$ ou $u\langle 0$ et $i\rangle 0(u \times i\langle 0)$
Dipôle ohmique 
$$
u_R=-\mathrm{R} \times i
$$
• Si $D$ est un générateur $u>0$ et $i>0 \quad(u \times i>0)$
Générateur de tension 
$$
u_{P N}=E-r i
$$
a) dispositif expérimental
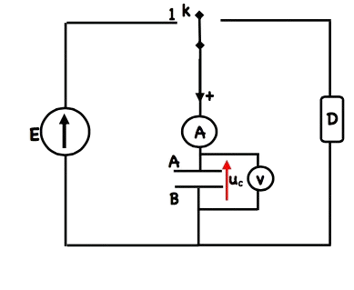
$k$ : interrupteur à deux positions
A : ampèremètre à aiguille centrale (galvanomètre)
$G$ : source de tension continue de f.e.m $E$
$D$ : conducteur ohmique de résistance $R$
b) charge du condensateur
k est fermé en position (1) :
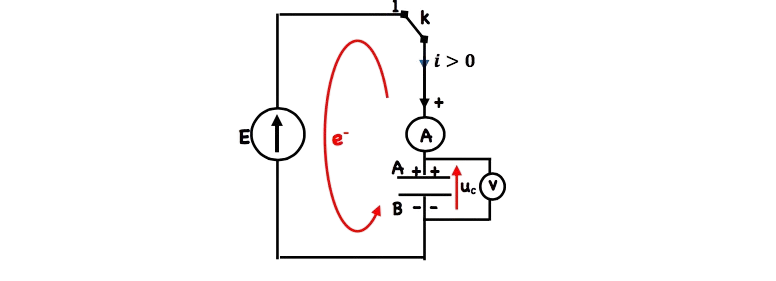
L’ampèremètre indique le passage d’un courant dans le sens positif, donc on a un déplacement d’ede l’armature $A$ vers $B$, ce qui amène une charge $q>0$ qui augmente sur l’armature $A$ et $-q$ sur l’armature $B$ et le voltmètre indique une tension qui augmente progressivement.
On dit que le condensateur se charge.
A la fin de la charge, le courant s’annule et la tension $u_c$ se stabilise sur la valeur de E
c) décharge du condensateur
$K$ est fermé en position 2 :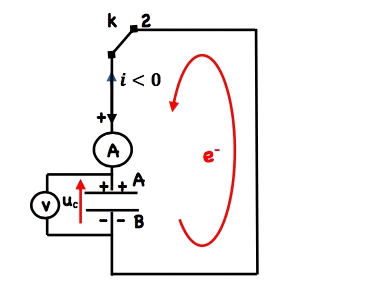
L’ampèremètre indique le passage d’un courant dans le sens négatif, donc on a un déplacement d’e- de l’armature $B$ vers $A$, par conséquence la charge $q$ du condensateur diminue et le voltmètre indique une tension qui diminue progressivement.
On dit que le condensateur se décharge.
À la fin de la décharge, le courant et la tension du condensateur s’annulent
Remarque
À la fin de la charge ou de la décharge les $e^{-}$cessent de se déplacer donc le courant s’annule.
2. Relation entre la charge $q$ et l’intensité du courant.
𓄲 À un instant $t$ la charge du condensateur est $q$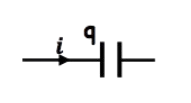
𓄲 À l’instant $t+d t$ la charge du condensateur est $q+d q$
Donc dq est la variation de charge pendant la durée dt , ce qui donne un courant d’intensité algébrique :
$$
i=\frac{d q}{d t} \quad\left(1 A=1 c v^{-1}\right)
$$
Remarque
✹ Pendant la charge, la valeur de q augmente avec le temps donc l’intensité $\boldsymbol{i}>\mathbf{0}$.
✹Pendant la décharge, la valeur de q diminue avec le temps donc l’intensité $\boldsymbol{i}<\mathbf{0}$.
✹ À la fin de la charge ou de la décharge, q est constante donc l’intensité $\boldsymbol{i}=0$.
✹ Pour un courant d’intensité constante : $\quad I=\frac{\Delta q}{\Delta t}$
3. Capacité du condensateur.
a) Expérience
le montage représenté sur le schéma est formé de :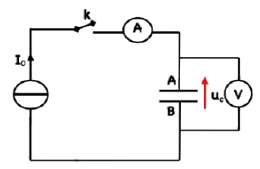
✹ Un condensateur déchargé .
✹ Un voltmètre, un ampèremètre
✹ Un générateur idéal de courant qui délivre un courant constant $\mathrm{I}_0$ d’intensité constante.
À un instant $t=0$, on ferme l’interrupteur $k$ et on note la valeur de la tension $u_c$ au borne du condensateur à des instants différents.
pour un courant de $I=10 \mu A$, les résultats sont les suivants :
$$
\begin{array}{|c|c|c|c|c|}
\hline t(\mathrm{~s}) & 0 & 8 & 16 & 24 \\
\hline u_c(V) & 0 & 4 & 8 & 12 \\
\hline
\end{array}
$$
b) Utilisation des résultats
On constate que la tension $u_c$ est proportionnelle au temps t. $\mathrm{u}_{\mathrm{c}}=\mathrm{k} . t$ et on $\mathrm{a} \mathrm{I}=\frac{q}{t}$ donc $\boldsymbol{u}_c=\frac{I}{k} q$. donc $q=\frac{I}{k}, u_c$
La charge $q$ du condensateur est proportionnelle à la tension $u_c$ entre ses bornes.
Le facteur de proportionnalité est la capacité du condensateur noté $C$ son unité est le farad.
donc
$$
q=C . u_c \quad(1 c=1 F V)
$$
Remarque
on $a \quad i=\frac{d q}{d t} \quad$ et $\quad q=C \times \mathrm{u}_{\mathrm{c}} \quad$ donc $\quad i=c \cdot \frac{d u_c}{d t}$.
4. association de condensateurs
↬1er cas
a) en série
On a $\quad i=\frac{d q_1}{d t}=\frac{d q_2}{d t}=\frac{d q}{d t} \quad$ donc $\quad q_1=q_2=q$
On a aussi $\mathrm{u}_1+\mathrm{u}_2=\mathrm{u} \quad \Rightarrow \quad \frac{q_1}{\boldsymbol{c}_1}+\frac{q_2}{C_2}=\frac{q}{C_{e q}} \quad \Rightarrow \quad \frac{1}{C_1}+\frac{1}{C_2}=\frac{1}{C_{e q}}$
cas général $\frac{1}{c_{e q}}=\sum \frac{1}{c_i}$ le montage en série permet de diminuer la valeur de $C$.
↬2éme cas
b) en parallèle
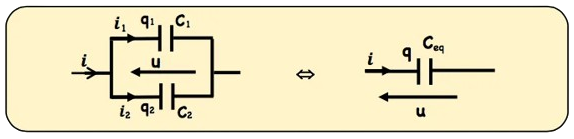
$$
\begin{aligned}
\text { on a } i_1+i_2=i \quad & \Rightarrow q_1+q_2=q \quad \Rightarrow \quad c_1 \cdot \mathbf{u}+c_2 . \mathrm{u}=c_{e q} . \mathrm{u} \\
& \Rightarrow \quad c_1+c_2=c_{e q}
\end{aligned}
$$
Cas général
$c_{e q}=\sum c_i$ le montage en parallèle permet d’augmenter la valeur de $c$.
II. Réponse d'un dipôle RC soumis à un échelon de tension.
1) Échelon de tension.
Un échelon de tension est une tension électrique qui passe instantanément :
𓄲 De 0 à une tension constante $E$ (échelon ascendant).
𓄲 D’une la valeur $E$ à la valeur 0 (échelon descendant)
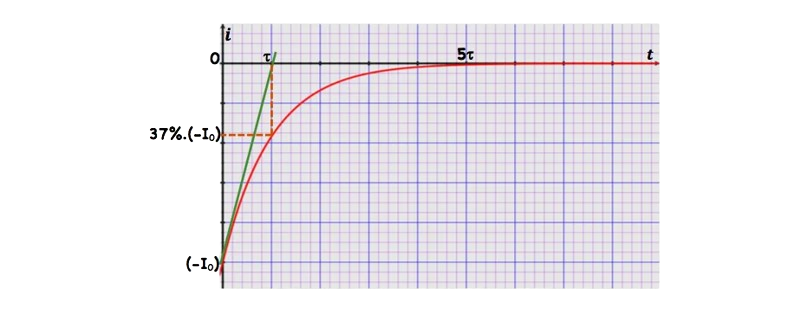
2) le montage expérimentale
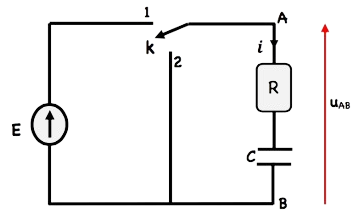
✹ lorsque $k$ passe de 2 à 1 , la tension $u_{A B}$ passe de 0 à $E$
(échelon ascendant)
✹ le passage de $k$ de 1 à 2 , la tension $u_{A B}$ passe de $E$ à 0
(échelon descendant)
3) la phase de charge du condensateur.
a) Équation différentielle vérifiée par la tension $u_c$.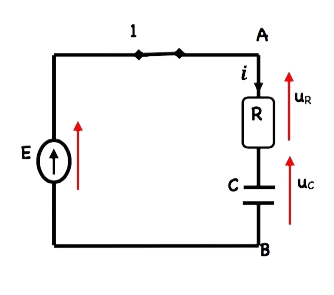
À $t=0$, on bascule l’interrupteur $k$ de 2 à 1 .
La loi d’additivité des tensions appliquée aux bornes du dipôle
$R C$ permet d’écrire: $u_R+u_C=E \Rightarrow R i+u_c=E$
donc l’équation différentielle cherchée s’écrit: $R C \cdot \frac{d u_c}{d t}+u_c=E$
b) solution d’équation différentielle.
La solution générale de l’équation différentielle précédente est $u_c(t)=A \cdot e^{-t / \tau}+B$
$A, B$ et $\tau$ sont des constantes à déterminer.
Pour déterminer les constantes A, B et $\tau$ il faut suivre les étapes suivantes:
↬ 1er étape
On remplace la solution dans l’équation différentielle
Donc: RC. $\underbrace{)}_{\frac{d u_c}{d t} \cdot \frac{-1}{\tau} e^{-t / \tau}}+\underbrace{A \cdot e^{-t / \tau}+B}_{\mathbf{u}_c}=E \Rightarrow\left(1-R C \cdot \frac{1}{\tau}\right) \cdot A e^{-t / \tau}=E-B$.
Pour que cet équation soit vérifié $\forall t$ il faut que : $\Rightarrow \underbrace{\left(1-R C \cdot \frac{1}{\tau}\right)}_{=0} \cdot A e^{-t / \tau}=\underbrace{E-B}_{=0}$
Donc $\tau=R C$ et $B=E$
↬2éme étape
Les conditions initiales : à $t=0$ on $a u_c=0$ (le condensateur est déchargé) donc
$$
A+B=0 \Rightarrow A=-B=-E \text { donc } \quad u_c(t)=E .\left(1-e^{-t / \tau}\right)
$$
Remarques
☉ L’analyse dimensionnelle
⊹ $\tau=\mathrm{RC} \Rightarrow[\tau]=[\mathrm{R}] \cdot[\mathrm{C}] \Rightarrow[\tau]=[\mathrm{u}] \cdot[\mathrm{I}]^{-1} \cdot[\mathrm{I}] \cdot[\mathrm{u}]^{-1} \cdot[\mathrm{~T}]=[\mathrm{T}]=\mathbf{s}$
$\tau$ est appelée la constante du temps du circuit
☉ $\vdash$ La constante du temps
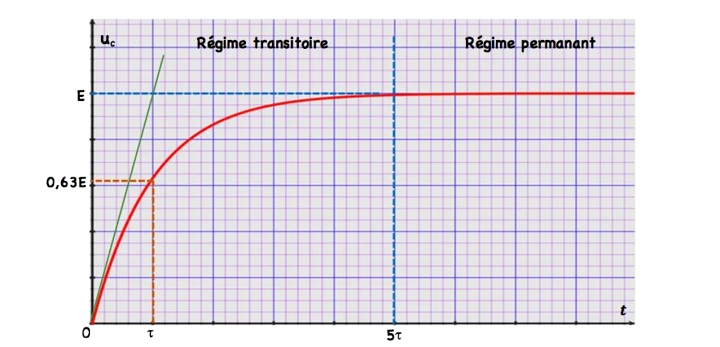
⊹ $u_c(\tau)=E .\left(1-e^{-1}\right) \Rightarrow u_c(\tau)=63 \% \cdot E$
$\tau$ est la durée au bout de laquelle le condensateur est chargé à $63 \%$.
☉ la détermination de la constante du temps graphiquement
⊹ $\tau$ est l’abscisse du point d’intersection de la tangente à la courbe à $t=0$ et la tangente à l’m.
☉ La durée de charge
⊹ $u_c(5 \tau)=E .\left(1-e^{-5}\right) \Rightarrow u_c(5 \tau)=99,4 \%$. $E$
donc au bout de $(5 \tau)$ on peut considérer que le condensateur est totalement chargé.
C) l’intensité de courant de charge.
$$
\left.\begin{array}{ll}
\text { on a } & i=c . \frac{d u_c}{d t} \\
& u_c(t)=E .\left(1-e^{-t / \tau}\right)
\end{array}\right\} \quad i=\frac{E}{R} e^{-t / \tau}
$$
Remarques
• $i(0)=\mathrm{I}_0=\frac{E}{R}$ et $i(\propto)=0$
• $\quad i(t)>0 \quad \forall t$.
• $\boldsymbol{i}(\tau)=37 \% . \mathrm{I}_0$
• $\quad i(5 \tau) \approx 0$
4) Ia phase de décharge du condensateur.
a) Équations différentielles vérifiée par la tension $u_c$.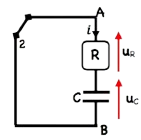
À un instant $t=0$ on bascule $k$ de 1 à 2 , Le courant circule dans le sens négatif ( mais on garde la même convention récepteur).
La loi d’additivité des tensions appliquée aux bornes du dipôle $R C$ permet d’écrire : $u_R+u_c=0 \Rightarrow R i+u_c=0$. donc l’équation différentielle s’écrit :
$$
R C \cdot \frac{d u_c}{d t}+u_c=0
$$
$$
\rfloor_B
$$
b) solutions des équations différentielles.
La solution générale de l’équation différentielle précédente est $u_c(t)=A \cdot e^{-t / \tau}+B$
$A, B$ et $\tau$ sont des constantes à déterminer.
Pour déterminer les constantes A, B et $\tau$ il faut suivre les étapes suivantes:
↬1er étape
On remplace la solution dans l’équation différentielle
Donc: $R C \cdot(\underbrace{\left(A \cdot \frac{-1}{\tau} e^{-t / \tau}\right.}_{\frac{d u_c}{d t}})+\underbrace{A \cdot e^{-t / \tau}+B}_{u_c}=0 \quad \Rightarrow \quad\left(1-R C \cdot \frac{1}{\tau}\right) \cdot A e^{-t / \tau}=-B$.
Pour que cet équation soit vérifié $\forall t$ il faut que : $\Rightarrow \underbrace{\left(1-R C \cdot \frac{1}{\tau}\right)}_{=0} \cdot A e^{-t / \tau}=\underbrace{-B}_{=0}$
Donc
$$
\tau=R C \text { et } B=0
$$
↬2éme étape
Les conditions initiales : à $t=0$ on a $u_c=E$ (le condensateur est chargé) donc
$$
A+B=E \quad \Rightarrow \quad A=E \text { donc } \quad u_c(t)=E \cdot e^{-t / \tau}
$$
Remarques
• $u_c(0)=E ; u_c(\propto)=0$.
•$u_c(\tau)=37 \% . E$ donc $\tau$ est la durée au bout de laquelle le condensateur est déchargé de $63 \%$ de sa valeur initiale
c) l’intensité de courant de décharge.
$\left.\begin{array}{cc}\text { on a } & i=c . \frac{d u_c}{d t} \\ u_c(t)=E . e^{-t / \tau}\end{array}\right\} \quad i(t)=-\frac{E}{R} e^{-t / \tau}$
Remarques
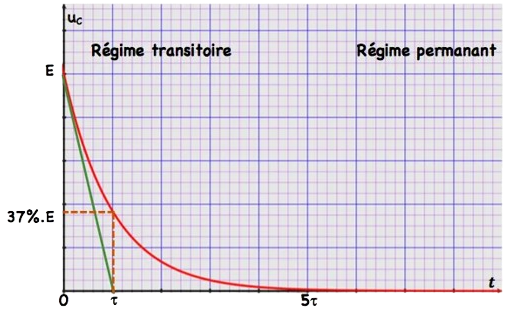
• $i(0)=-\mathrm{I}_0=-\frac{E}{R}$ et $i(\propto)=0$
• $i(t)<0 \quad \forall t$.
• $i(\tau)=37 \% .\left(-I_0\right)$.
• On a $i(t)\left\langle 0\right.$ et $\left.u_c(t)\right\rangle O$ donc le condensateur fonctionne en générateur
Conclusion
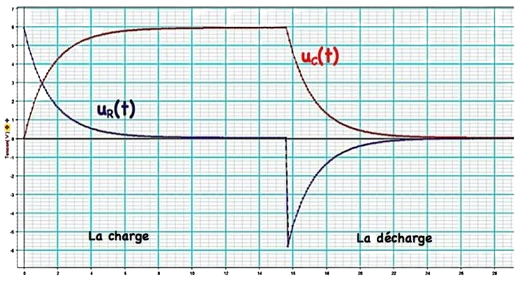
Ia tension au borne du condensateur est une fonction continue en fonction du temps et le courant passant par le condensateur est discontinue.
III. Énergie emmagasinée dans un condensateur.
1. Puissance électrique du condensateur
La puissance reçue par le condensateur est $\mathcal{P}=u_c i$
$$
\Rightarrow \quad P=c \cdot u_c \frac{d u_c}{d t} \quad \Rightarrow \quad P=\frac{1}{2} c \cdot \frac{d u_c^2}{d t} \quad \Rightarrow \quad P=\frac{d\left(\frac{1}{2} c c_c^2\right)}{d t} .
$$
2. l’énergie électrique emmagasinée dans le condensateur
$\xi_e(t)$ est L’énergie emmagasinée dans un condensateur de capacité $C$ aux bornes duquel règne une tension $u_c$.
$$
\left.\begin{array}{cc}
\text { on a : } & \mathcal{P}=\frac{d\left(\xi_c\right)}{d t} \\
& \mathcal{P}=\frac{d\left(\frac{1}{2} c u_c^2\right)}{d t}
\end{array}\right\} \stackrel{\text { par primitive }}{\Longrightarrow} \xi_e=\frac{1}{2} . c . \boldsymbol{u}_c^2+\mathrm{Cte}
$$
Et pour $u_c=0$ on a $\xi_e=0$ donc la $C+e=0$.
D’où :
$$
\xi_e=\frac{1}{2} \cdot c \cdot u_c^2=\frac{1}{2} \frac{q^2}{c}
$$
↬ l’expression de l’énergie en fonction du temps
$$
\begin{array}{|c|c|}
\hline \text { Pendant la charge } & \text { Pendant la décharge } \\
\hline \xi_e(t)=\frac{1}{2} c \cdot E^2\left[1-e^{-t / \tau}\right]^2 & \xi_e(t)=\frac{1}{2} c \cdot E^2 e^{-2 t / \tau} \\
\hline
\end{array}
$$
↬La courbe de la variation de l’énergie du condensateur au cours de la décharge
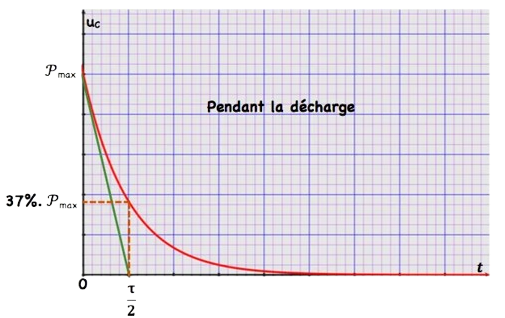
– Exercice 1
Un condensateur initialement déchargé est inséré dans le circuit (Figure 1):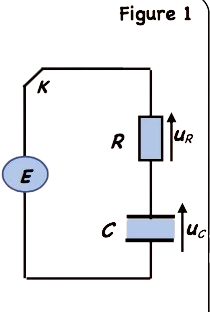
Le conducteur ohmique a une résistance $R=100 \Omega$. On veut alors déterminer la capacité $C$ du condensateur et la tension E du générateur.
1. $\grave{A} t=O s$ on ferme l’interrupteur K. Établir l’équation différentielle vérifiée par $u_c(t)$.
2.Vérifier que $u_c(t)=A\left(1-e^{-t / \tau}\right)$ est bien une solution de cette équation différentielle.
Montrer alors que: $\ln \left(E-u_c\right)=\ln (E)-\dagger / \tau$.
3. La figure (2) donne la variation de $\ln \left(E-u_c\right)$ en fonction de $t$.
Trouver graphiquement la valeur des grandeurs $E$ et $\tau$.
4. On note $\xi e(\tau)$ l’énergie électrique emmagasinée dans le condensateur à la date $t=\tau$, et $\xi e_{(\text {max }}$ l’énergie électrique maximale du condensateur.
Calculer le rapport $\xi e(\tau) / \xi \boldsymbol{e}_{(\text {max })}$.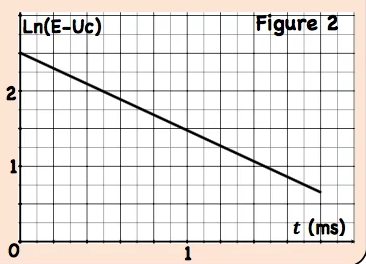
5. On insère un autre condensateur de capacité $C^{\prime}$. Le circuit a donc une constante de temps égale à $\tau^{\prime}=\tau / 3$.
Le condensateur $C^{\prime}$ est-il-inséré en série ou en parallèle? justifier la réponse et déterminer la valeur de $C^{\prime}$.
On considère un condensateur de capacité $C=1 \mu \mathrm{~F}$, deux résistors de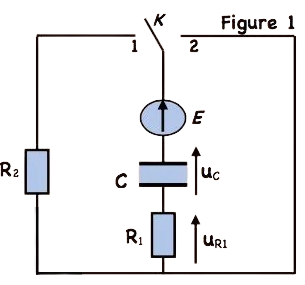
résistances $R_1$ et $R_2$, un commutateur $k$ et un générateur de tension de f.e.m $E$. On réalise le schéma du circuit de la figure-1-. Avant chaque expérience, on décharge complètement le condensateur.
Expérience 1: A l’instant $t=0$, on place le commutateur k sur la position 1.
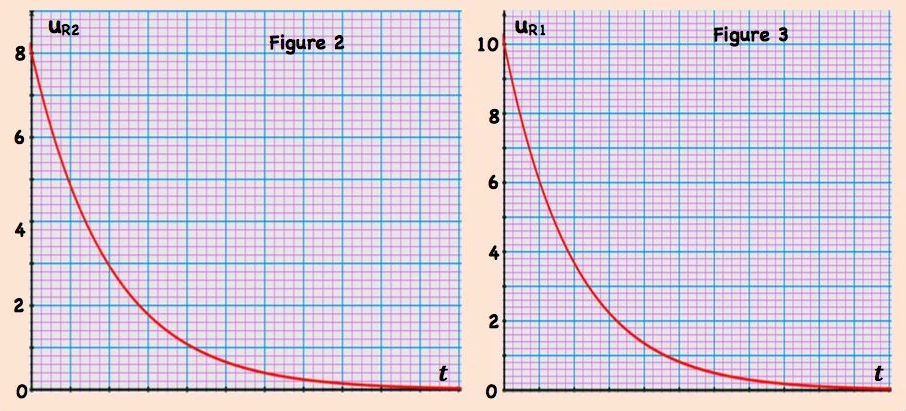
Un oscilloscope à mémoire permet d’enregistrer les variations de la tension $u_{R 2}(t)$ aux bornes du résistor de résistance $R_2$ comme l’indique l’oscillogramme de la figure-2-
1- a) Établir l’équation différentielle vérifiée par la tension $u_{R 2}(t)$ et montrer qu’elle s’écrit sous la forme : $\frac{\mathrm{du}_{\mathrm{R} 2}}{\mathrm{dt}}+\frac{1}{\tau} \cdot \mathrm{u}_{\mathrm{R} 2}=0$; où $\tau$ est une constante qu’on exprimera en fonction de $R_1, R_2$ et $C$.
b) La tension $u_{R 2}(t)=$ A. $e^{-\alpha t}$, est une solution de l’équation différentielle. Déterminer l’expression de :
* $A$ en fonction de $R_1, R_2$ et $E$.
${ }^* \alpha$ en fonction de $R_1, R_2$ et $C$.
2- Déduire l’expression de la tension $u_c(t)$.
3- Montrer que: $\tau=\frac{\mathrm{EC}}{8} \cdot \mathrm{R}_2$.
Expérience 2: A un nouvel instant $t=0$, on bascule le commutateur $k$ sur la position 2. L’oscillogramme de la figure-3-, représente les variations de la tension $u_{\text {R1 }}(t)$ aux bornes du résistor de résistance $\mathbf{R}_1$. L’équation différentielle régissant les variations de l’intensité du courant $i(t)$ s’écrit sous la forme: $\frac{\mathrm{di}}{\mathrm{dt}}+10^3 . i=0$.
La solution de cette équation différentielle est $i(t)=10^{-2} . e^{-t / \tau^{\prime}}$ où $\tau^{\prime}$ est la constante de temps d’expression $\tau^{\prime}=\mathbf{R}_{\mathbf{1}} \mathbf{C}$.
