Vectors and translation
I- Direction and sense
1. The Direction :
Exemple :
– We consider the following figures :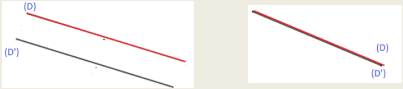 
– The two lines (D) and (D’) are parallel lines or superposable lines, so they have the same direction
Définition :
▶ A line in the plane determine a direction
▶ Two lines (D) and (D’) have the same direction if (D) and (D’) are parallel lines or superposable lines.
▶ If Two lines (D) and (D’) are secants lines then the two lines (D) and (D’) haven’t the same direction.
Exemple :
– We consider the following figures :
– The two lines (d) and (d’) are parallel, so they have the same direction.
– The two lines ( $\Delta$ ) and ( d ) are secant lines, so they haven’t the same direction.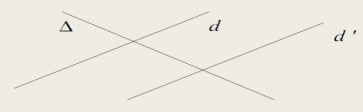
Remark :
► Two distinct(different) points $A$ and $B$ determine one direction which is the line (AB) and all the parallel lines to the line $(A B)$.
2. The sense :
Définition :
– We consider the line (AB) or (d)
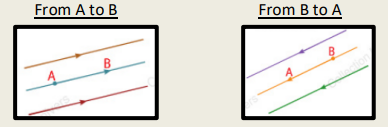
– We can determine two possible senses in the line (AB)
▶ Sense 1 : From A to B.
▶ Sense 2 : From B to A.
Remark :
► Attention : the word direction in our daily life is confused with the sense, In MATH we choose the direction (the line) first then we choose the sense.
– Two distinct(different) points A and B determine in the direction of the line (AB) two opposites senses indicated with arrows,
II- The vector
Définition :
A vector is a geometrical entity ; it’s a combination of three things :
– A direction (a line) in space,
– A sense from the tail to the head.
– A positive number called its magnitude,
– Typically, a vector is illustrated as a directed straight line.
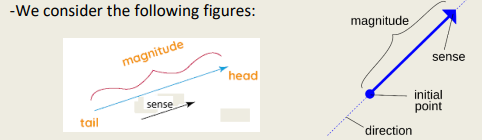
The vector in this example $\overrightarrow{A B}$ with :
✓ $\checkmark$ The direction of the vector $\overrightarrow{A B}$ which is the line ( AB )
✓ $\checkmark$ The sense of the arrow, from the point A to the point B ,
✓ $\checkmark$ The magnitude of $\overrightarrow{A B}$ given by the length of the distance AB .
✓ $\checkmark$ The origine (Tail or origine point) which is the point A
✓ $\checkmark$ The head (the extremity or the arrowhead) which is the point B
Exemple :
Remark :
❖ A vector can be represented by a line with an arrow pointing towards its sense and its length represents the magnitude of the vector.
❖ Vectors are represented by arrows; they have initial points and terminal points.
❖ Every two distinct points A and B determine two vectors : $\overrightarrow{A B}$ and $\overrightarrow{B A}$
$\begin{aligned} & \text { The vector } \overrightarrow{A B} \text { is } \\ & \text { characterized by: }\end{aligned}\left\{\begin{array}{l}\text { The direction: }(\mathrm{AB}) \\ \text { The sense: } \mathrm{A} \Rightarrow \mathrm{B} \\ \text { The magnitude : the distance } \mathrm{AB}\end{array}\right.$
1. The null/zero vector :
Définition :
► A vector with no direction and no sense and magnitude equal to 0 is known as null or zero vector
► Every point in the plane determines a vector called null vector
► We write : $\overrightarrow{A A}=\overrightarrow{0}$
► If $\overrightarrow{A B}=\overrightarrow{0} \quad$ Then $\quad \mathbf{A}=\mathbf{B}$ (The two points $\mathbf{A}$ and $\mathbf{B}$ are the same point)
► If $\overrightarrow{A B}=\overrightarrow{0} \quad$ Then $\quad \overrightarrow{A B}=\overrightarrow{A A}=\overrightarrow{B B}=\overrightarrow{0}$
2. The opposite of a vector :
Définition :
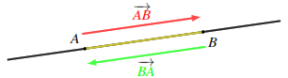
► A and B are two distinct points of the plane.
► We have : $\overrightarrow{A B}+\overrightarrow{B A}=\overrightarrow{0}$
► The vector $\overrightarrow{B A}$ is the opposite vector of the vector $\overrightarrow{A B}$
And we write: $\overrightarrow{B A}=-\overrightarrow{A B}$
Exemple :
We consider the following figure :
III- Equal vectors
Définition :
► Two vectors are equal if they have:
– The same direction
– The same sense
– The same magnitude
► $\overrightarrow{A B} \overrightarrow{C D}$ if:
– $\overrightarrow{A B}$ and $\overrightarrow{C D}$ have the same direction; ( $\mathbf{A B}$ )//(DC)
– $\overrightarrow{A B}$ and $\overrightarrow{C D}$ have the same sense; $[\mathrm{AB})$ and $[\mathrm{DC})$ have the same sense
– $\overrightarrow{A B}$ and $\overrightarrow{C D}$ have the same magnitude; $\mathbf{A B}=\mathbf{D C}$
Exemple :
– We consider the following figures :
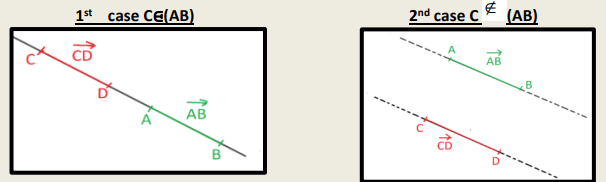
Remark :
❖ The equality $\overrightarrow{A B} \overrightarrow{C D}$ regroup three conditions, the three conditions (the direction, the sense, the magnitude) should be verified to say that: $\overrightarrow{A B} \overrightarrow{C D}$
Propriety :
If $\overrightarrow{A B}=\overrightarrow{D C}$
Then : $\quad-\mathrm{ABCD}$ is a parallelogram
$-[\mathrm{AC}]$ and $[\mathrm{BD}]$ have the same midpoint
Exemple :
– We consider the following figure :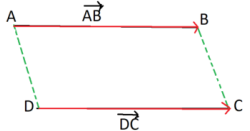
– We have $\overrightarrow{A B}=\overrightarrow{D C}$
– Then $(\mathrm{AB}) / /(\mathrm{DC})$ and $\mathrm{AB}=\mathrm{DC}$
– So : ABCD is a parallelogram
– The diagonals $[A C]$ and $[B D]$ have the same midpoint
Propriety 2 :
If ${A B C D}$ is a parallelogram Then $\quad \overrightarrow{A B}=\overline{D C}$
Exemple :
– We consider the following figure :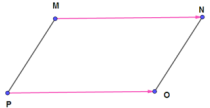
– We have MNOP is a parallelogram
– Then $\overrightarrow{M N}=\overrightarrow{P O}$ and $\overrightarrow{M P}=\overrightarrow{N O}$
Propriety 3 :
If $\overrightarrow{A B} \overrightarrow{A D}$ Then $B=D$
Propriety 4 :
If $\overrightarrow{A B}=\overrightarrow{B C}$ Then B is the midpoint of the segment $[\mathrm{AC}]$
If $\overrightarrow{B A}=\overrightarrow{C B}$ Then B is the midpoint of the segment $[\mathrm{AC}]$
IV- The sum of vectors
1. The sum of vectors (Triangle method) :
Définition :
► The vectors addition (Triangle method)
– To add two vectors $\overrightarrow{A B}$ and $\overrightarrow{B C}$ we follow the steps :
Step 1 : Draw the vector $\overrightarrow{A B}$
Step 2 : At the head (the arrowhead) of $\overrightarrow{A B}$, draw the vector $\overrightarrow{B C}$.
Step 3 : Join the beginning of $\overrightarrow{A B}$ to the head (the arrowhead) of $\overrightarrow{B C}$
► This is vector $\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}$
Exemple :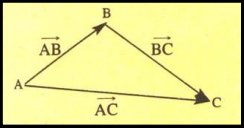
– We consider the following figure :
– $\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}$
The sum of two vectors is a vector
2. The sum of vectors (Parallelogram method) :
Définition :
► The vectors addition (Parallelogram method)
– The sum of the two vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$ is the vectors $\overrightarrow{A E}$ such as :
► ABEC is a parallelogram
Exemple :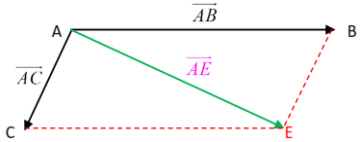
– We consider the following figure :
– $\overrightarrow{A B}+\overrightarrow{A C}=\overrightarrow{A E}$
The sum of the two vectors is the diagonal of
the parallelogram
Proprieties :
► $\overrightarrow{A B}, \overrightarrow{C D}$ and $\overrightarrow{E F}$ are non null vectors
► The sum of vectors is commutative :
$$
\overrightarrow{A B}+\overrightarrow{C D}=\overrightarrow{C D}+\overrightarrow{A B}
$$
► The sum of vectors is summative :
$$
\overrightarrow{(\overrightarrow{A B}+\overrightarrow{C D})}+\overrightarrow{E F}=\overrightarrow{A B}+(\overrightarrow{C D}+\overrightarrow{E F})
$$
► The sum of the zero vector :
$$
\overrightarrow{A B}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{A B}=\overrightarrow{A B}
$$
3. CHASLES theorem :
Rule :
– We have :
$$
\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}
$$
Exemple :
– We consider the following figure :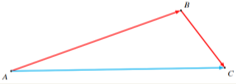
– $\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}$
Exemple 2 :
Without drawing simplify the following expressions :
$\begin{aligned} \overrightarrow{E F}+\overrightarrow{G E}+\overrightarrow{F G} & =\overrightarrow{E F}+\overrightarrow{F G}+\overrightarrow{G E} \\ & =\overrightarrow{E G}+\overrightarrow{G E} \\ & =\overrightarrow{E E} \\ & =\vec{O}\end{aligned}$
$\begin{aligned} \overrightarrow{A B}-\overrightarrow{B D}+\overrightarrow{C A}-\overrightarrow{C B} & =\overrightarrow{A B}+\overrightarrow{D B}+\overrightarrow{C A}+\overrightarrow{B C} \\ & =\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C A}+\overrightarrow{D B} \\ & =\overrightarrow{A C}+\overrightarrow{C A}+\overrightarrow{D B} \\ & =\overrightarrow{A A}+\overrightarrow{D B} \\ & =\vec{O}+\overrightarrow{D B} \\ & =\overrightarrow{D B}\end{aligned}$
4. The sum of many vectors :
Rule :
– We have :
$$
\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}
$$
5. The Midpoint of a segments :
Rule :
– We have: $\overrightarrow{A M}+\overrightarrow{B M}=\overrightarrow{0}$
$$
\begin{aligned}
& \overrightarrow{M A}+\overrightarrow{M B}=\overrightarrow{0} \\
& \overrightarrow{A M}=\frac{1}{2} \overrightarrow{A B} \\
& \overrightarrow{A B}=\mathbf{2} \times \overrightarrow{A M}=\mathbf{2} \times \overrightarrow{M B}
\end{aligned}
$$
V- Vectors Subtract
Définition :
► $\overrightarrow{A B}$ and $\overrightarrow{C D}$ are non null vectors
► To subtract two vectors we add the opposite vector of the second vector
$\begin{aligned} \overrightarrow{A B}-\overrightarrow{C D}= & \overrightarrow{A B}+(-\overrightarrow{C D}) \\ & =\overrightarrow{A B}+\overrightarrow{D C}\end{aligned}$
► $\overrightarrow{A B}-\overrightarrow{C D}$ is called the difference between the two vectors $\overrightarrow{A B}$ and $\overrightarrow{C D}$
Exemple :
– We have : A, B and C are three distinct points.
– Let’s calculate $\overrightarrow{A B}-\overrightarrow{A C}$
$\begin{aligned} \overrightarrow{A B}-\overrightarrow{A C} & =\overrightarrow{A B}+(-\overrightarrow{A C}) & & \rightarrow \text { Using the definition of subtract } \\ & =\overrightarrow{A B}+\overrightarrow{C A} & & \rightarrow \text { Using the definition opposite vectors } \\ & =\overrightarrow{C A}+\overrightarrow{A B} & & \rightarrow \text { We can change the order of vectors } \\ & =\overrightarrow{C B} & & \rightarrow \text { Using CHASLES theorem }\end{aligned}$
VI- Vectors Multiplication
Rule :
– We have : $\overrightarrow{A B}+\overrightarrow{A B}+\ldots \ldots \ldots \ldots+\overrightarrow{A B}=\mathbf{n} \times \overrightarrow{A B}$
Exemple :
– We have : $\quad \overrightarrow{A B}+\overrightarrow{A B}+\overrightarrow{A B}=3 \times \overrightarrow{A B} \quad$ and $\quad(-\overrightarrow{M N})+(-\overrightarrow{M N})=(-2) \times \overrightarrow{M N}$
Remark :
❖ $\overrightarrow{A B}$ is a non null vector and $\mathbf{n}$ is an integer; $\mathbf{n} \times \overrightarrow{A B}=(-\mathbf{n}) \times \overrightarrow{B A}$
VII- Translation
Définition :
► When we drag(move) a figure (1) from point E to point K in a straight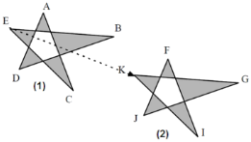
line without turn it, to get the figure (2)
– We say that : the figure (2) is the image of the figure (1) with translation that transforms the point $E$ to the point K or with respect to the Vector $\overrightarrow{E K}$
Définition :
► A, B and M are distinct points of the plane :
►$\overrightarrow{A B}$ is a non null vector
► We say that: the point M’ is the image of point M with translation that transforms the point $\mathbf{A}$ to the point $\mathbf{B}$ (or with respect to the Vector $\overrightarrow{A B}$ ) if $\quad \overrightarrow{A B}=\overrightarrow{M M^{\prime}}$
► We note : $t_{\overline{A B}}(\mathbf{M})=\mathbf{M}^{\prime}$
► It means that :
– The two lines (AB) and (MM’) have the same direction
– The sense from $M$ to $M$ ‘ is the same sense from $A$ to $B$
– The two distances AB and $\mathrm{MM}^{\prime}$ are equal
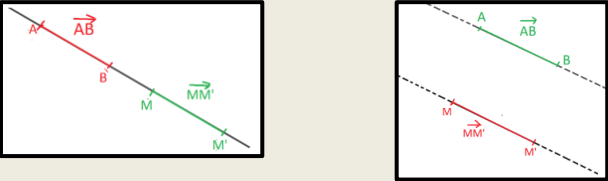
Exemple :
$\overrightarrow{A B}$ is a non null vector. M and $\mathrm{M}^{\prime}$ are points such $\overrightarrow{M M^{\prime}}=\overrightarrow{A B}$
– the point $\mathbf{M}^{\prime}$ is the image of point $\mathbf{M}$ with translation that transforms the point $\mathbf{A}$ to the point B (or with respect to the Vector $\overrightarrow{A B}$ )
Remark :
❖ $\overrightarrow{A B}$ is a non-null vector. M and $\mathrm{M}^{\prime}$ are points such $\overrightarrow{M M^{\prime}}=\overrightarrow{A B}$
❖ the point $\mathbf{M}^{\prime}$ is the image of point $\mathbf{M}$ with translation that transforms the point $\mathbf{A}$ to the point $B$ (or with respect to the Vector $\overrightarrow{A B}$ )
❖ Means that : $\mathbf{A B M} \mathbf{M}$ is a parallelogram
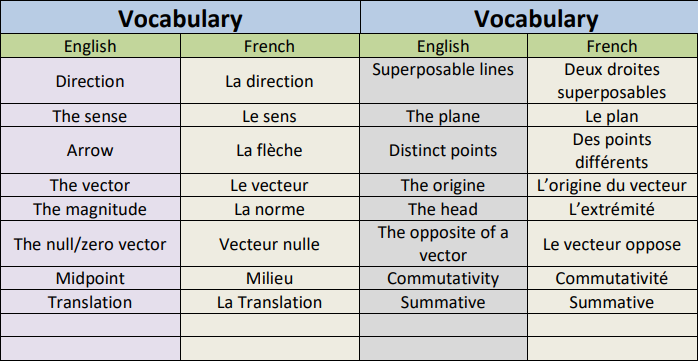
VIII- Vocabulary
