The right triangle and the circle
I- The right triangle theorem
1. The right triangle direct theorem :
The right triangle direct theorem :
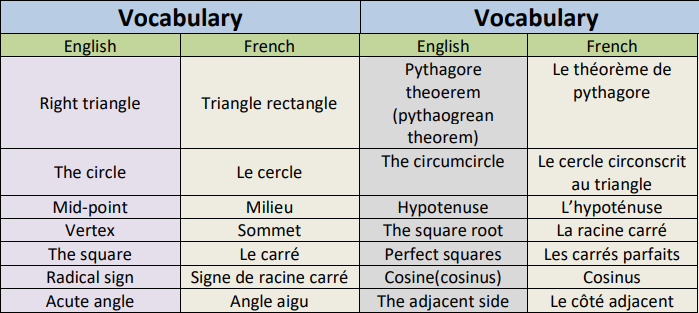
If ABC is a right triangle on the apex A and I is the midpoint of [BC]
Then : $I A=I B=I C=\frac{B C}{2}$
Exemple :
– ABC is a right triangle on the apex A and I is the midpoint of $[\mathrm{BC}]$ -We deduce that :
$$
I A=I B=I C=\frac{B C}{2}
$$
The right triangle direct theorem: (in other words)
If ABC is a right triangle
Then : the mid-point of its hypotenuse is equidistant to all the vertexes of this triangle
$\left.\begin{array}{l}\text { IF: } A B C \text { is a right triangle } \\ \text { on the apex } A \\ \text { I is the mid-point } \\ \text { the hypotenuse }[B C]\end{array}\right\} \begin{aligned} & \text { Then: } I A=I B=I C=\frac{B C}{2} \\ & \end{aligned}$
2. The right triangle direct theorem reciprocal :
The right triangle direct theorem reciprocal :
If ABC is a triangle and I is the midpoint of [BC]
such as : $\quad I A=I B=I C=\frac{B C}{2}$
Then : ABC is a right triangle on the apex A
Exemple :
– $A B C$ is a triangle $M$ is the midpoint of $[B C]$ such as $M A=M B=M C$
– We deduce that: ABC is a right triangle on the apex A
The right triangle direct theorem reciprocal : (in other words)
If in a triangle the midpoint of one triangle’s side is equidistant to all the triangle’s vertexes
Then : the triangle is a right triangle
$\left.\begin{array}{rl}\text { IF: } & A B C \text { is a triangle } \\ & I \text { is the mid-point of } \\ & \\ \text { the hypotenuse }[B C] & \\ & \text { and } I A=I B=I C=\frac{B C}{2}\end{array}\right\} \quad$ Then : $\frac{A B C \text { is a right triangle }}{\text { on the apex } A}$j,
II- The circumcircle to the right triangle
1. The right triangle and the circumcircle direct theorem :
The right triangle and the circumcircle direct theorem :
If $A B C$ is a right triangle on the apex $A$ and $I$ is the midpoint of $[B C]$
Then : The circle with center I and radius IB is the circumcircle of the right triangle ABC
Exemple :
– ABC is a right triangle on the apex A
– O is the midpoint of $[\mathrm{BC}]$ such as $\mathrm{OA}=\mathrm{OB}=\mathrm{OC}=\frac{B C}{2}$
– We deduce that : $\mathrm{C}\left(\mathrm{O} ; \mathrm{OA}=\frac{B C}{2}\right)$ is the circumcircle to the triangle ABC
The right triangle and the circumcircle direct theorem : (in other
words)
If one triangle is a right triangle
Then : the triangle’s hypotenuse and its mid-point are the diameter and center of the triangle’s circumcircle
2. The right triangle and the circumcircle direct theorem reciprocal :
The right triangle and the circumcircle direct theorem reciprocal :
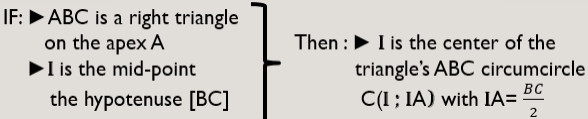
If [BC] is the circle’s (C) diameter and A is an element of the circle (C )
Then : ABC is a right triangle on the apex A
Exemple :
– (S) is a circle with center O and diameter [BC]
$A B C$ is a right triangle on the apex $A$ because $[B C]$ is the diameter of the circle (S)
MBC is a right triangle on the apex M because $[\mathrm{BC}]$ is the diameter of the circle (S)
The right triangle and the circumcircle direct theorem reciprocal : (in other words)
If A is an element of a circle with diameter [BC]
Then : ABC is a right triangle on the apex A
III- The pythagor theorem (The Pythagorean theorem)
1. The square root
Définition :
► The square of a number is the product of a number and itself.
– Ex : the square of 5 is 25
Exemple :
Find the square of 3 .
$3 \cdot 3=9 \quad$ Multiply 3 by itself.
So, the square of 3 is 9 .
Remark :
Numbers like 9, 16, and 225 are called square numbers or perfect squares because they are
squares of whole numbers.
Définition :
► The square root of a number are the same factors multiplied to form perfect squares.
► A radical sign $\sqrt{ }$, is the symbol used to indicate a square root.
Words A square root of a number is one of its two equal factors.
Examples
Numbers
$4 \cdot 4=16$, so $\sqrt{16}=4$.
Algebra
If $x \cdot x$ or $x^2=y$, then $\sqrt{y}=x$.

Remark :
Only positive integers have square roots, (the reason will be studied next year)
– So : a square root is always positive
$\$ \mathbf{a}$ and $\mathbf{b}$ are positive integers : $\sqrt{a^2 \times b}=a \sqrt{b}$
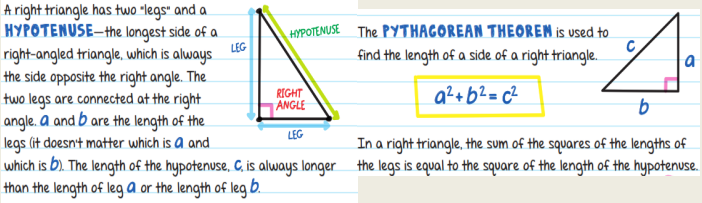
2. The pythagore theorem (The Pythagorean theorem)
The pythagore theorem
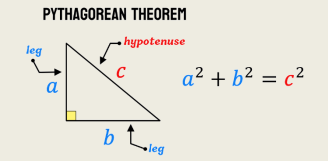
If $A B C$ is a right triangle on the apex $A$
Then : $B C^2=A B^2+A C^2$
The pythagore theorem (in other words)
If $\mathbf{A B C}$ is a right triangle on the apex $\mathbf{A}$
Then : the square of its hypotenuse is equal to the sum of the others sides’ squares
Exemple :
Remark :
✦ IF ABC is a right triangle on the apex A then : $\mathrm{AC}<\mathrm{BC}$ and $\mathrm{AB}<\mathrm{BC}$
✦ IF $A B C$ is a right triangle on the apex $B$ then : $\mathbf{A C}^{\mathbf{2}}=\mathbf{A B}^{\mathbf{2}}+\mathbf{B C}^{\mathbf{2}}$
✦ IF ABC is a right triangle on the apex C then : $\mathbf{A B}^{\mathbf{2}}=\mathbf{A C}^{\mathbf{2}}+\mathbf{B C}^{\mathbf{2}}$
✦ The pythagor theorem is used to calculate the length of a side knowing the two other sides
of the right triangle
IV- The cosinus(cosine) of an acute angle
Définition :
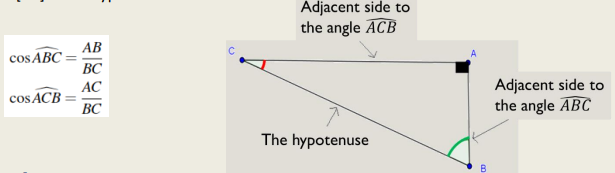
► In a right triangle, the cosinus(cosine) of an acute angle is equal to the quotient of the length of the adjacent side to that angle over the length of the hypotenuse
► $\cos$ angle $=\frac{\text { the length of the adjacent side to the angle }}{\text { the length of the hypotenuse }}$
Exemple :
– ABC is a right triangle on the apex A
– The quotient : $\frac{A C}{B C}$ is called the cosinus(cosine) of the angle $A C B$
– We write : $\cos A \hat{C} B=\frac{A C}{B C}$
Vocabulary :
❖ ABC is a right triangle on the apex A
❖ $A C B$ and $A B C$ are acute angles
❖ $[\mathrm{AB}]$ is the adjacent side to the angle $A \hat{B} C$ and the opposite side to the angle $A \hat{C} B$
❖ $[\mathrm{AC}]$ is the adjacent side to the angle $A \hat{C} B$ and the opposite side to the angle $A \hat{B} C$
❖ [BC] is the hypotenuse
Remark :
– The cosinus(cosine) of any angle is always positive and inferior to 1 ;
– if $x$ is the measure of an acute angle, then $0<\cos (x)<1$
– The quotient cos has no unit,
$\cos 60^{\circ}=\frac{1}{2} \quad ; \quad \cos 0^{\circ}=1 \quad ; \quad \cos 90^{\circ}=0$
Propriety 1 :
Then: $\cos ^2(A \hat{B} C)+\cos ^2(A \hat{C} B)=1$
Exemple :
$\cos ^2 33^{\circ}+\cos ^2 57^{\circ}=1 \quad ; \quad \cos ^2 20^{\circ}+\cos ^2 70^{\circ}=1$
Propriety 2 : (general case)
Then: $\cos ^2(\alpha)+\cos ^2(90-\alpha)=1$
Propriety 3 :
– If $\boldsymbol{\alpha}=\boldsymbol{\beta}$
Then: $\cos (\alpha)=\cos (\beta)$
Exemple :
– We consider the following figure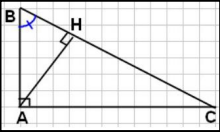
– We have : $A \hat{B} C=A \hat{B} H$
– So : $\cos A \hat{B} C=\cos A \hat{B} H$
– Then : $\frac{A B}{B C}=\frac{B H}{A B}$
– Finally : $\mathrm{AB}^2=\mathrm{BH} \times \mathrm{BC}$
V- VOCABULARY