Proportionality and linear functions
I- Recognizing proportionality
Exemple :
– We Consider the following table :
$$
\begin{array}{|l|c|c|c|c|}
\hline 7 & 4 & 5.4 & 11 & 2.5 \\
\hline 21 & 12 & 16.2 & 33 & 7.5 \\
\hline
\end{array}
$$
– We say : there’s a proportionality in this table (also : this table represents a proportionality situation).
– The terms in the second line are found by multiplying the terms in the first line by the same number 3
– We have : $\frac{21}{7}=\frac{12}{4}=\frac{16.2}{5.4}=\frac{33}{11}=\frac{7.5}{2.5}=3$
– The number 3 is called the proportionality coefficient
Définition :
▶ Proportionality occurs in a table (Or the table represent a proportionality situation) when the terms in one line are obtained by multiplying or dividing those in the other line by the same non-null number.
▶ This number is called the proportionality coefficient.
Remark :
– We Consider the following table :
– Note that this table does not represent proportionality, as it does not have the same proportionality coefficient.
$$
\begin{array}{|c|c|c|}
\hline 5 & 1 & 8 \\
\hline 15 & 10,7 & 2 \\
\hline
\end{array}
$$
II- Graphical representation of proportionality
Exemple :
– We Consider the following table :
$$
\begin{array}{|l|c|c|c|}
\hline \text { Number of kg of apples } & 0,5 & 1 & 1.5 \\
\hline \text { Price(dh) } & 1,5 & 3 & 4.5 \\
\hline
\end{array}
$$
– We have : $\frac{1,5}{0,5}=\frac{3}{1}=\frac{4,5}{1,5}=3$
– So, this table represents a situation of proportionality
– In an orthogonal plan ( $0 ; \mathrm{I}$; J), let’s represent the points: $\mathrm{A}(0.5 ; 1.5) ; \mathrm{B}(1 ;$ 3) ; C(1.5; 4.5)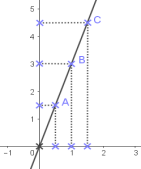
-Note that all points: $A$; $B$ and $C$ are aligned with the origin of the orthogonal plan ( $O ; I ; J$ ),
– We say : the figure represents a situation of proportionality.
Exemple :
– We Consider the following table :
$$
\begin{array}{|l|c|c|c|}
\hline \text { Nbre of kg of potatos } & 1 & 3 & 4 \\
\hline \text { The price(dh) } & 2 & 6 & 7 \\
\hline
\end{array}
$$
– We have : $\frac{2}{1}=1$ and $\frac{6}{3}=2$ and $\frac{7}{4}=1.75$
– So, this table doesn’t represent a situation of proportionality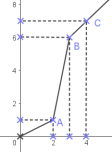
– In an orthogonal plan ( $O ; I ; J)$, let’s represent the points : $A(1 ; 2)$; $\mathrm{B}(2 ; 3) ; \mathrm{C}(3 ; 6)$
– Note that all points: A; B and C aren’t aligned with the origin of the orthogonal plan ( $\mathrm{O} ; \mathrm{I} ; \mathrm{J}$ ),
– We say : the figure doesn’t represent a situation of proportionality.
Propriety :
III- The fourth proportional
Exemple :
– We Consider the following table :
$$
\begin{array}{|c|l|}
\hline 14,5 & 25 \\
\hline Y & 5 \\
\hline
\end{array}
$$
– We have $2 \times 1,5=3$ and $5 \times 1,5=7,5$
– So, this table represent a situation of proportionality
– Now let’s calculate the CROSS PRODUCT : $2 \times 7,5=15$ and : $3 \times 5=15$
– We say that 7,5 is the fourth proportional of the numbers 2; 3 and 5 .
Définition :
▶ $\mathbf{b}$; b; c and $\mathbf{x}$ are non-null integers
▶ x is the fourth proportional of the numbers a ; b and c means :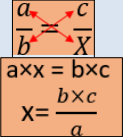
Exemple :
– We Consider the following table :
– This table represent a situation of proportionality
$$
\begin{array}{|c|l|}
\hline 14,5 & 25 \\
\hline \mathrm{Y} & 5 \\
\hline
\end{array}
$$
– So $\quad \frac{14,5}{V}=\frac{25}{5}$;
– Then $25 \times Y=14,5 \times 5$
– Finally, $Y=\frac{14.5 \times 5}{25}=2,9$
IV- Uniform Movement/ Uniform motion
Exemple :
– We Consider the following table :
$$
\begin{array}{|l|c|c|}
\hline \text { Time(hours) } & 2,5 & 4 \\
\hline \text { Distance(km) } & 200 & 320 \\
\hline
\end{array}
$$
– This table represent a situation of proportionality
– We have $200 \div 2,5=80 ; 320 \div 4=80$
– So : the speed is constant
– The Speed is $80 \mathrm{~km} / \mathrm{h}$
– We say : the movement is uniform/Uniform motion
Exemple 2 :
– We Consider the following table :
$$
\begin{array}{||c|c|c||}
\hline \text { Time(hours) } & 2 & 5 \\
\hline \text { Distance(km) } & 140 & 300 \\
\hline
\end{array}
$$
– We have $140 \div 2=70 ; 300 \div 5=60$
– So : the speed is not constant
– We say : the movement isn’t uniform
The speed isn’t constant
Définition :
▶ A movement is uniform/Uniform motion when we move at constant speed.
▶ Movement is uniform/Uniform motion if the travel time is proportional to the distance covered.
V- The scale
Exemple :
– We Consider the following scale :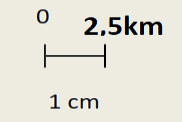
– 1 cm on this plan represents 2.5 km in reality,
– 1 cm on this plan represents 250000 cm in reality.
– We say : $\underline{\text { The scale }}=\frac{1}{250000}$
Définition :
▶ The scale of a plan is the coefficient of proportionality between distances on the plan and actual distances, expressed in the same units.
▶ The scale $=\frac{\text { Distanceethemap }}{\text { Actualdistancereality }}$
▶ The scale $=\frac{d}{D}$
Exemple 2 :
– We Consider the following table :
$$
\begin{array}{|c|c|c|}
\hline \begin{array}{c}
\text { Distance in the } \\
\text { map (cm) }
\end{array} & 125 & \mathrm{y} \\
\hline \begin{array}{c}
\text { Distance in reality } \\
(\mathrm{Km})
\end{array} & \mathrm{x} & 75 \\
\hline
\end{array}
$$
– Let’s find the value of x and y ?
$\begin{array}{lc}\frac{1}{250000}=\frac{125}{x} & \frac{1}{250000}=\frac{y}{75} \\ x=\frac{250000 \times 125}{1} & y=\frac{75 \times 1}{250000} \\ x=31250000 \mathrm{~cm} & y=0,0003 \mathrm{~cm} \\ : x=312,5 \mathrm{~km} & : y=30 \mathrm{~cm}\end{array}$
VI- The percentage
Exemple :
– In a school with 650 students, $12 \%$ of students come by bus.
– What is the number of those students ?
$\begin{aligned} 12 \% \text { of } 650 & =\frac{12}{100} \times 650 \\ & =(650 \div 100) \times 12 \\ & =6,5 \times 12 \\ & =78 .\end{aligned}$
Rule :
Calculating $\mathbf{x \%}$ of a quantity $\mathbf{n}$ is equivalent to multiplying this number $\mathbf{n}$ by $\frac{x}{100}$
The percentage $\mathbf{X}$ of the number $n$ is $n \times \frac{x}{100}$
VII- Linear function
Définition :
▶ $\mathbf{a}$ is a rational number,
▶ Any relation that link a rational number $\mathbf{x}$ by the product $\mathbf{a x x}$ is called a linear function.
▶ we write : $\quad \mathbf{f}: \mathbf{x} \longrightarrow \mathbf{a x}$. Or we write : $\mathbf{f}(\mathbf{x})=\mathbf{a x}$
▶ we say : $a x$ is the image of $x$ by the function $f$ and the number $\underline{a}$ is the coefficient of the linear function f
Exemple :
– We consider the following proportionality table

– The coefficient of proportionality is the number $\mathbf{3}$
– So : $\mathbf{y = 3} \times \mathbf{x}$
– The relation between the number $\mathbf{x}$ and its image $\mathbf{y}$ is called the linear function $f$
– We write : $\mathbf{f}(\mathbf{x})=\mathbf{3} \times \mathbf{x}$ or $\mathbf{f}(\mathbf{x})=\mathbf{y}$
– the number $\mathbf{3}$ is the coefficient of the linear function $\mathbf{f}$
– The number $3 \times x$ is the image of $x$ by the linear function $f$
Exemple :
– We consider the following linear function $f$ such as : $f(x)=-\mathbf{2 x}$
– Let’s calculate the image of $\mathbf{1}$
– We have $\quad \boldsymbol{f}(\boldsymbol{x})=-\mathbf{2} \boldsymbol{x}$
– so $\quad f(1)=-2 \times 1$
– Then, $\quad f(\mathbf{1})=-\mathbf{2}$
Remark :
– We have : $f(x)=a x$
– The linear function $\underline{f}$ represents a situation of proportionality and the number $\underline{a}$ is the coefficient of proportionality
– the number $\underline{a}$ is the coefficient of the linear function $f$
1. The coefficient of the linear function f
Exemple :
– We consider the following linear function $f$ such as: $f(x)=-3 x$
– Let’s calculate $\frac{f(2)}{2}$ and $\frac{f(-5)}{-5}$
– We have $f(x)=-3 x$
– so $\quad \frac{f(2)}{2}=\frac{-3 \times 2}{2}=-3$
– And $\quad \frac{f(-5)}{-5}=\frac{-3 \times-5}{-5}=-3$
– So, for any rational number $\mathrm{x}: \quad a=\frac{f(x)}{x}=-3$
Propriety :
a is a rational number,
We consider the following linear function $f$ such as: $f(x)=a x$
So : $\quad \mathbf{a}=\frac{f(x)}{x}$ is the coefficient of the linear function $\mathbf{f}$
Exemple :
– We consider the following linear function $f$ such as: $f(x)=\mathbf{4 x}$
– Let’s calculate $\frac{f(2)-f(1)}{2-1}$ and $\frac{f\left(\frac{1}{2}\right)-f(0)}{\frac{1}{2}-0}$
– We have $\mathbf{f}(\mathbf{x})=\mathbf{4 x}$
– so $\quad \frac{f(2)-f(1)}{2-1}=\frac{8-4}{2-1}=\frac{4}{1}=4$
– And $\quad \frac{f\left(\frac{1}{2}\right)-f(0)}{\frac{1}{2}-0}=\frac{2-0}{\frac{1}{2}-0}=2 \times 2=4$
– So, for any rational number x and $\mathrm{x}^{\prime}$ with $\mathrm{x} \neq \mathrm{x}^{\prime}$
$$
a=\frac{f(x)-f\left(x^{\prime}\right)}{x-x^{\prime}}
$$
Propriety :
➤ $\mathbf{a}$ is a rational number,
➤ We consider the following linear function $f$ such as : $f(x)=a x$
➤ for any rational number x and $\mathrm{x}^{\prime}$ with $\mathrm{x} \neq \mathrm{x}^{\prime}$
$\mathbf{a}=\frac{f(\mathrm{x})-f\left(\mathrm{x}^{\prime}\right)}{\mathrm{x}-\mathrm{x}^{\prime}}$ is the coefficient of the linear function $\mathbf{f}$
2. The graphic presentation of the linear function f
Exemple :
– We consider the following linear function $f$ such as: $f(x)=-3 x$
– We have:
$$
\begin{array}{|c|c|c|c|}
\hline x & 1 & 0 & -1 \\
\hline f(x) & -3 & 0 & 3 \\
\hline
\end{array}
$$
– Let’s plot the points $\mathrm{A}(-1 ; 3) ; \mathrm{B}(1 ;-3)$ and $\mathrm{C}(0 ; 0)$ in the orthogonal plan,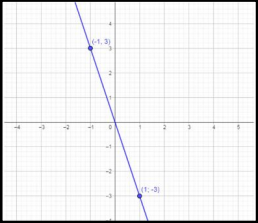
Remarque
– We have : $\mathbf{f}(\mathbf{x})=-\mathbf{3 x}$
– The points $\mathrm{A}(-1 ; 3) ; \mathrm{B}(1 ;-3)$ and $\mathrm{C}(0 ; 0)$ are aligned points,
The line ( $A B$ ) is the graphical presentation of the function $f$