Dosage acido-basique
I. Dosage acido-basique
1) Principe d’un dosage acido-basique
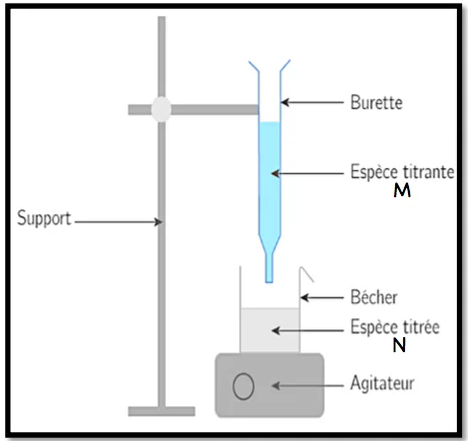
Doser (ou titrer) une espèce chimique $M$ en solution c’est déterminer sa quantité de matière ou sa concentration au moyen d’une réaction chimique.
Pour cela on fait réagir totalement l’espèce $M$ de la solution à doser (solution titrée de concentration inconnue) avec une espèce $N$ d’une solution titrante (réactif dont on connaît la concentration)
Une réaction support de dosage doit être :
– Rapide.
– Totale ( le réactif limitant doit être toujours entièrement consommé ).
– Spécifique de l’espèce à doser ( $N$ ne doit réagir qu’avec $M$ et non avec les autres espèces en solution).
2) Équivalence d’un titrage.
Considérons une réaction de titrage acido-basique modélisée par l’équation suivante :
$$
A_1 H_{a q}+A_2^{-}{ }_{a q} \rightarrow A_1^{-}{ }_{a q}+A_2 H_{a q}
$$

Soit $V_2$ le volume versé de la solution titrante et $V_{2 E}$ le volume versé à l’équivalence.
⊹ Si $V_2\left\langle V_{2 E}\right.$ (avant l’équivalence) le réactif titrant est limitant ( $x_{\max }=C_2 V_2$ ): $\left.C_1 V_1\right\rangle C_2 V_2$
⊹ Si $\left.V_2\right\rangle V_{2 E}$ (après l’équivalence ) le réactif titré est limitant $\left(x_{\max }=C_1 V_1\right): C_1, V_1\left\langle C_2 V_2\right.$
⊹ Si $V_2=V_{2 E}$ (à l’équivalence) les deux réactifs son limitants donc $x_{\max }=n_0$ (acide) $=n_{0 E}$ (base)
la relation d’équivalences est $C_1 \cdot V_1=C_2 V_{2 E}$
II. Le dosage PH-métrique.
1) Dosage de l’acide éthanoïque par une solution d’hydroxyde de sodium.
– L’acide éthanoïque réagit partiellement avec l’eau: $\mathrm{CH}_3 \mathrm{COOH}_{a q}+\mathrm{H}_2 \mathrm{O}_{\mathrm{L}} \leftrightarrows \mathrm{CH}_3 \mathrm{COO}^{-}{ }_{\text {aq }}+\mathrm{H}_3 \mathrm{O}^{+}{ }_a$
– L’hydroxyde de sodium est une base qui réagit totalement avec l’eau : $\mathrm{NaOH}_{(s)} \rightarrow \mathrm{Na}^{+}$aq $+\mathrm{HO}^{-}$
a) expérience.
On introduit dans un bécher à l’aide d’une pissette jaugée un volume $V_a=20 \mathrm{ml}$ d’une solution $S_a d^{\prime}$ acide éthanoïque à titrer de concentration $C_a$ ?, puis on lui ajoute progressivement à l’aide d’une burette la solution titrante $S_b$ d’hydroxyde de sodium de concentration $C_b=0,1$ mol. $L^{-1}$ tout en utilisant un Système d’agitation afin d’homogénéiser le mélange.
b) résultats
Par un pH-mètre plonge dans le bécher on mesure le PH du mélange pour chaque volume $\mathrm{V}_{\mathrm{b}}$ versé, on obtient les résultats suivants à $25^{\circ} \mathrm{C}$ :
$$
\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline \mathrm{V}_{\mathrm{b}}(\mathrm{ml}) & 0 & 2 & 4 & 8 & 10 & 14 & 18 & 19 & 19,5 & 20 & 20,5 & 21 & 24 & 28 & 32 & 38 \\
\hline \mathrm{pH} & 2,9 & 3,8 & 4,2 & 4,6 & 4,8 & 5,1 & 5,7 & 6,1 & 6,5 & 8,7 & 11 & 11,4 & 12 & 12,2 & 12,4 & 12,5 \\
\hline
\end{array}
$$
$$
\text { On a un saut de PH autour de } \mathrm{V}_{\mathrm{b}}=20 \mathrm{ml} \text {. }
$$
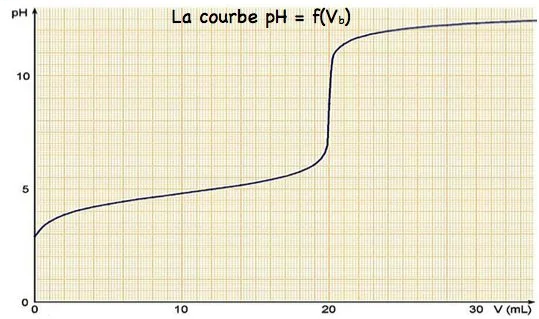
c) L’équation de réaction
$$
\mathrm{CH}_3 \mathrm{CO}_2 \mathrm{H}_{\mathrm{aq}}+\mathrm{HO}_{\mathrm{aq}}^{-} \rightarrow \mathrm{CH}_3 \mathrm{CO}_2^{-}{ }_{\mathrm{aq}}+\mathrm{H}_2 \mathrm{O}_{\mathrm{L}}
$$
La constante d’équilibre de la réaction : $\mathbf{k}=\frac{\left\lfloor\mathrm{CH}_3 \mathrm{CO}_2^{-}\right\rfloor .}{\left\lfloor\mathrm{CH}_3 \mathrm{CO}_2 \mathrm{H}\right] \cdot\left\lfloor\mathrm{HO}^{-}\right\rfloor}=\frac{\left\lfloor\mathrm{CH}_3 \mathrm{CO}_2^{-}\right\rfloor \cdot\left|\mathrm{H}_3 \mathrm{O}^{+}\right|}{\left.\left\lfloor\mathrm{CH}_3 \mathrm{CO}_2 \mathrm{H}\right] \cdot\left[\mathrm{HO}^{-}\right\rfloor\right\rfloor\left[\mathrm{H}_3 \mathrm{O}^{+}\right\rfloor}$donc $\mathbf{K}=\frac{\mathrm{K}_A}{K_e}$
$$
k=\frac{1,6 \cdot 10^{-5}}{10^{-14}}=1,6.10^9 \text { alors la réaction est totale. }
$$
d) Détermination du point d’équivalence
La détermination du point d’équivalence $E$ peut se faire de plusieurs manières.
i) Méthode des tangentes : À partir du tracé de la courbe $\mathrm{pH}=\mathrm{f}\left(\mathrm{V}_{\mathrm{b}}\right)$ :
Autour du point d’équivalence (point d’inflexion) :
• on trace une tangente $\left(T•1\right)$ à la courbe juste avant l’équivalence,
• on trace la tangente $\left(T_2\right)$ juste après l’équivalence, et qui est parallèle à la tangente $\left(T_1\right)$,
• on trace un segment orthogonal aux deux tangentes $\left(T_1\right)$ et $\left(T_2\right)$,
• on marque le milieu $M$ de ce segment,
• on trace la droite ( $D$ ), parallèle aux deux tangentes $\left(T_1\right)$ et $\left(T_2\right)$ et passant par $M$. La droite (D) coupe la courbe en un point $E$, c’est le point d’équivalence de coordonnés $E\left(V_{B E} ; p H_E\right)$.
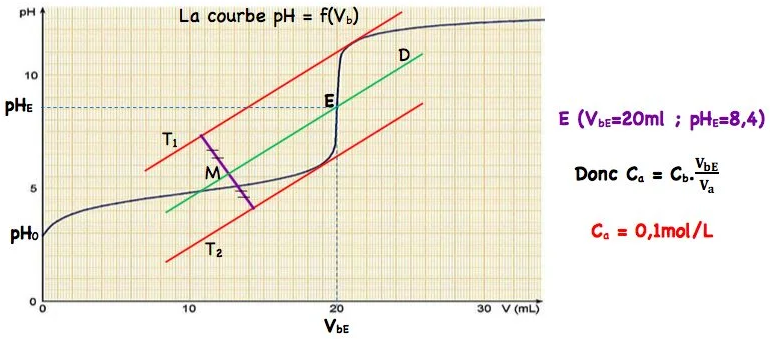
– Remarques
• le $\mathrm{pH}_0$ correspond au PH de la solution titrée.
• À l’équivalence on obtient une solution de $\left(\mathrm{Na}^{+}+\mathrm{CH}_3 \mathrm{CO}_2{ }^{-}\right)$donc la solution à l’équivalence est basique PHE $>7$
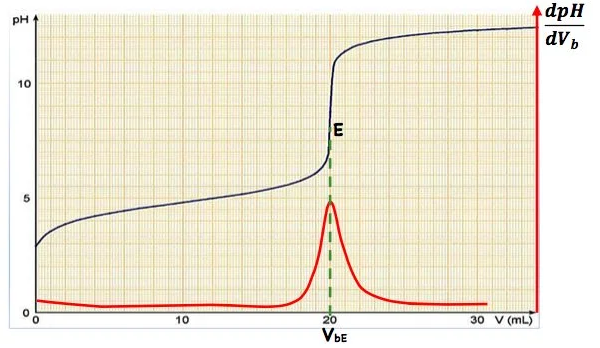
ii) Méthode de la dérivée : À partir du tracé de la courbe $\frac{d p H}{d V_h}=f\left(V_b\right)$
Au point d’équivalence, le PH fait un saut (un point d’inflexion), donc sa dérivée est maximal. donc $I^{\prime}$ abscisse du pic est $\mathrm{V}_{\mathrm{BE}}$.
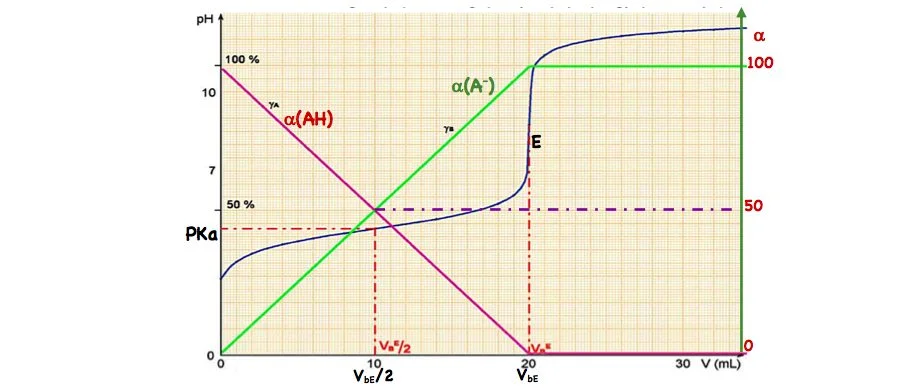
iii) À partir du tracé du pourcentage.
On peut aussi utiliser des courbes représentants le pourcentage de présence de l’acide de la base dans le mélange en fonction du volume ajouté.
$$
\alpha(A H)=\frac{\lfloor A H]}{[A H]+\left\lfloor A^{-}\right\rfloor} \quad, \quad \alpha\left(A^{-}\right)=\frac{\left\lfloor A^{-}\right\rfloor}{\lfloor A H]+\left\lfloor A^{-}\right\rfloor}
$$
Avant l’équivalence et d’après le tableau d’avancement on a:
![]()
Remarques
• $\alpha(A H)$ et $\alpha\left(A^{-}\right)$en fonction de $V_b$ sont des droite affines de pente respectivement $\left(-\frac{1}{V_b}\right)$ et $\left(\frac{1}{V_b}\right)$.
• $$
\text { * Pour } \mathrm{V}_{\mathrm{b}}=\frac{1}{2} \cdot \mathrm{~V}_{\mathrm{bE}} \text { on } \mathrm{a} \alpha(\mathrm{AH})=\alpha\left(\mathrm{A}^{-}\right) \text {ce qui donne } \mathrm{PH}=\mathrm{PKa}\left(\mathrm{CH}_3 \mathrm{CO}_2 \mathrm{H}^{-} / \mathrm{CH}_3 \mathrm{CO}_2^{-}\right) \text {. }
$$
2) Dosage de l’acide chlorhydrique par une solution d’hydroxyde de sodium.
𓄲 Le chlorure d’hydrogène réagit totalement avec l’eau: $\mathrm{HCl}_9+\mathrm{H}_2 \mathrm{O}_{\mathrm{L}} \rightarrow \mathrm{H}_3 \mathrm{O}^{+}{ }_{a q}+\mathrm{Cl}^{-}{ }_{\text {aq }}$
𓄲 L’hydroxyde de sodium est une base qui réagit totalement avec I’eau : $\mathrm{NaOH}_{(s)} \rightarrow \mathrm{Na}^{+}{ }_{\text {aq }}+\mathrm{HO}^{-}{ }_{a q}$
a) Expérience
On dose, à $25^{\circ} \mathrm{C}$, une solution d’acide chlorhydrique de concentration molaire $C_A$ et de volume $\mathrm{V}_{\mathrm{A}}=20,0 \mathrm{~mL}$ par une solution d’hydroxyde de sodium de concentration molaire connue $C_8=0,10 \mathrm{~mol} . \mathrm{L}^{-1}$. La sonde pH -métrique plongé dans le bécher permet de déterminer le PH du mélange pour chaque volume ajouté.
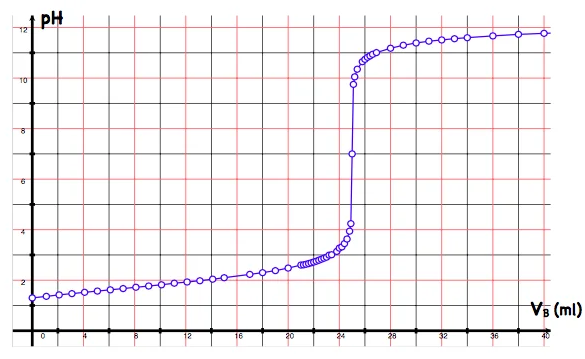
b) Équation de réaction
$\mathrm{H}_3 \mathrm{O}^{+}+\mathrm{HO}^{-} \rightarrow 2 \mathrm{H}_2 \mathrm{O} \quad$ La constante d’équilibre est $\mathrm{K}=1 / \mathrm{Ke}=10^{14}$, donc une réaction totale.
c) Détermination du point d’équivalence.
La méthode des tangentes
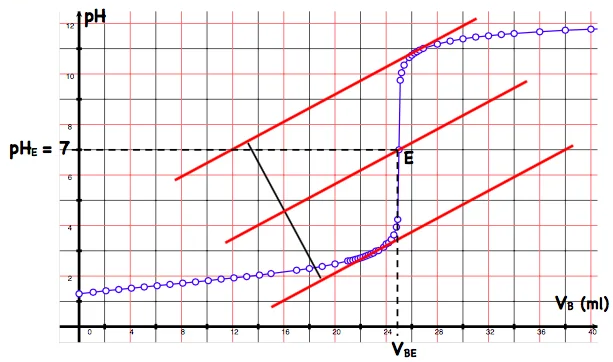
Le point d’équivalence $E\left(V_{B E}=25 \mathrm{ml} ; \mathrm{PHE}=7\right)$ donc $C_A=C_B V_{B E} / V_A=0,1 \times 25 / 20$
$$
C_A=0,125 \mathrm{~mol} / \mathrm{L}
$$
À l’équivalence on obtient une solution de chlorure de sodium ( $\mathrm{Na}^{+}+\mathrm{Cl}^{-}$) et $\mathrm{c}^{\prime}$ est une solution neutre donc $\mathrm{PH}_{\varepsilon}=7$.
III. Le dosage colorimétrique.
1- Dispositif
En absence d’un pH-métre, on peut utiliser un indicateur coloré.
2- Principe
Dans un dosage colorimétrique acido-basique. L’équivalence est repérée par le changement de couleur de l’indicateur coloré ajouté dans la solution.
3- Choix de l’indicateur coloré
Un indicateur coloré convenable pour repérer l’équivalence d’un titrage est un indicateur dont la zone de virage contient le $\mathrm{PH}_{\mathrm{E}}$ à l’équivalence
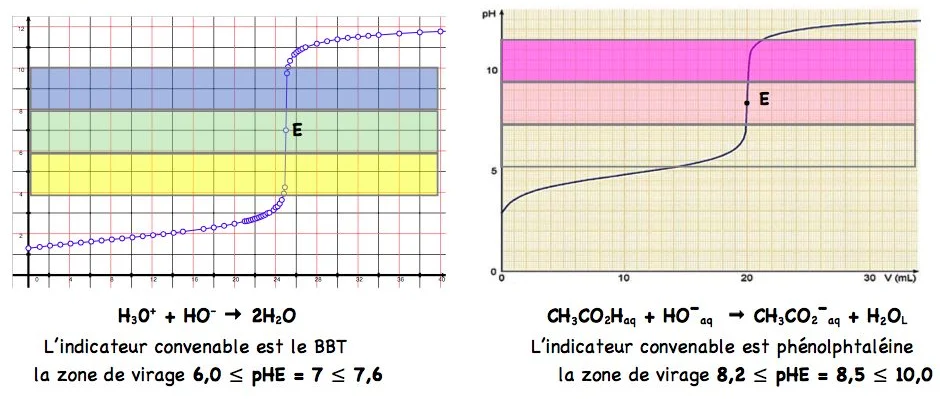
On dispose d’une solution S d’hydroxyde soude $\mathrm{Na}^{+}+\mathrm{HO}^{-}$de concentration C (inconnue).
On dilue 30 fois cette solution pour obtenir une solution $S^{\prime}$ de concentration $C^{\prime}$.
On introduit un volume $V_1=20 \mathrm{~mL}$ de solution $\mathrm{S}^{\prime}$ dans un bécher, que l’on dose par une solution $d^{\prime}$ acide chlorhydrique $\mathrm{Cl}^{-}+\mathrm{H}_3 \mathrm{O}^{+}$de concentration $\mathrm{C}_2=5,0 \times 10^{-3} \mathrm{~mol} . \mathrm{L}^{-1}$
On trouve un volume équivalent $\mathrm{V}_{\mathrm{E}}=12 \mathrm{~mL}$ :
calculer $C$, sachant que la réaction de dosage est une réaction acido-basique.
On dissout un comprimé < ibuprofène-400 » dans 40 mL d’eau.
On dose la solution obtenue par une solution d’hydroxyde de sodium $\mathrm{Na}^{+}+\mathrm{HO}^{-}$, de concentration $C_b=0,20 \mathrm{~mol} . \mathrm{L}^{-1}$, On trouve un volume équivalent $V_{\mathrm{E}}=9,7 \mathrm{~mL}$
L’ibuprofène sera noté R-COOH, de masse molaire $\mathrm{M}(\mathrm{R}-\mathrm{COOH})=206 \mathrm{~g} \cdot \mathrm{~mol}^{-1}$.
1) Donner les caractéristiques d’une équation de dosage.
2) Calculer $n_v$, la quantité d’hydroxyde de sodium versée à l’équivalence.
3) En déduire la masse d’ibuprofène contenue dans le comprimé.
– Dosage d’une base par un acide
Les amines sont des composés organiques qui se caractérisent par des solutions aqueuses basique. On s’intéresse à l’étude d’une solution aqueuse d’une amine $A$ de formule $C_2 H_5 \mathrm{NH}_2$.
On prépare une solution $S_0$ de cette amine de concentration $C_0=2.10^{-2} \mathrm{~mol} . \mathrm{L}^{-1}$ et de $\mathrm{pH}_0=11,55$ à $25^{\circ} \mathrm{C}$.
1-a) Écrire l’équation de réaction de l’amine $A$ avec l’eau, et dresser le tableau d’avancement.
-b) Calculer le taux d’avancement final de la réaction. Conclure.
-c) Calculer la valeur de $\mathrm{pK}_{\mathrm{A}}$ du couple acide/base de l’amine A .
2-On dilue, $n$ fois la solution $S_0$, pour obtenir une solution $S_1$ de concentration $C_1$.
On prend un volume $V_1=10 \mathrm{~mL}$ de la solution $\mathrm{S}_1$ et on procède au dosage avec une solution aqueuse d’acide chlorhydrique $\left(\mathrm{H}_3 \mathrm{O}^{+}+\mathrm{Cl}^{-}\right)$de concentration $\mathrm{C}_2=10^{-2} \mathrm{~mol} . \mathrm{L}^{-1}$.
L’évolution de la valeur de pH du mélange au cours du dosage, est représentée par la courbe ci-dessou
-a) Écrire l’équation de réaction du dosage et calculer sa constante d’équilibre.
Que peut-on dire de la nature de cette réaction?
-b) Déterminer les coordonnées du point d’équivalence
-c) Calculer la valeur de la concentration $C_1$ et déduire la valeur du facteur de dilution $n$.
-d) Justifier la nature de la solution à l’équivalence.
-e) Calculer les concentrations de l’amine $A$ et de son acide conjugué lorsqu’on a versé un volume $V_2=16 \mathrm{ml}$ de la solution titrante.
En déduire le pourcentage de chacun de l’amine $A$ et de son acide conjugué.