Etat d’équilibre d’un système chimique
I. Quotient de réaction Qr.
1. Définition.
Soit une transformation modélisée par l’équation suivant: $\quad a_{(a q)}+b B_{(a q)} \leftrightharpoons c C_{(a q)}+{d D_{(a q)}}$. le quotient de la réaction $Q_r$ est défini par: $\quad \mathbf{Q}_{\mathbf{r}}=\frac{[\mathbf{C}]^{\mathrm{c}}[\mathrm{D}]^{\mathrm{d}}}{[\mathbf{A}]^{\mathrm{a}}[\mathbf{B}]^{\mathrm{b}}}$
Remarque
$$
Q_R=\prod_{i=1}^N \alpha_i^{\nu_i}
$$
L’activité chimique d’une espèce est l’influence de la quantité d’une espèce sur l’énergie libre du système. Elle se définit schématiquement comme la « concentration active» de l’espèce en solution. Elle est :
– égale à 1 si l’espèce est un solvant, ou plus généralement une phase pure,
– égale à la concentration molaire de l’espèce sur la concentration de référence $C^{\circ}$ que l’on choisit égale à 1 mol. $\underline{L}^{-1}$ si l’espèce est un soluté,
– égale au rapport de la pression partielle (en bar) de l’espèce rapportée à une pression de référence $\mathrm{p}^{\circ}$ que l’on choisit égale à 1 bar si l’espèce est un gaz.
2. Propriétés.
a. Dans l’expression de $Q_r$, seules sont représentées les espèces en solution. Ce qui exclut les solides, les gaz non dissous et le solvant (l’eau).
b. Dans l’expression de $Q_r$, les concentrations des espèces en solution s’expriment en « mol. $L^{-1}$ » mais
$Q_r$ est une grandeur sans dimension
3. Exemples.
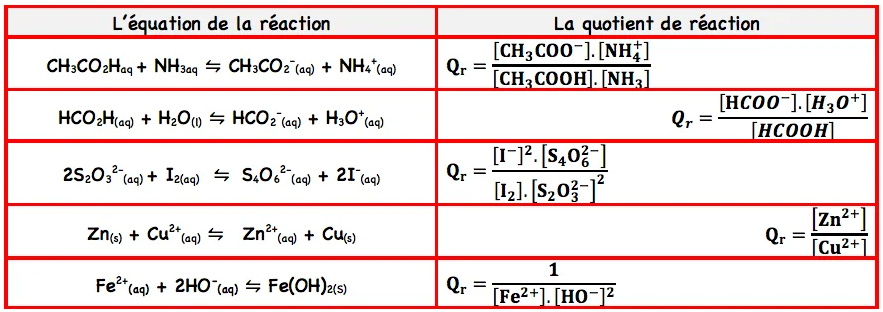
II. Quotient de réaction à l'état d'équilibre.
1. Définition.
Le quotient de réaction à l’état d’équilibre, noté $Q_{\text {réq }}$ ou $K$, est la valeur que prend le quotient de réaction lorsque l’état d’équilibre du système chimique est atteint.
$\AA 25^{\circ} \mathrm{C}$ on prend une solution $\mathrm{S}_1$ d’acide éthanoïque de concentration $\mathrm{C}_1=5.10^{-2} \mathrm{~mol} / \mathrm{L}$, sa conductivité est $\sigma_{e ́ q}=34,79 \cdot 10^{-3} \mathrm{~S} \cdot \mathrm{~m}^{-1}$.
Les ions présents dans la solution sont $A^{-}$et $\mathrm{H}_3 \mathrm{O}^{+}$.
la conductivité de la solution est : $\sigma_{e_q}=\lambda\left(H_3 O^{+}\right) \cdot\left[H_3 O^{+}\right]_{e q q}+\lambda\left(A^{-}\right) .\left[A^{-}\right]_{e_q}$
$$
\Rightarrow \quad \sigma_{\hat{e q}}=\left[\lambda\left(\mathrm{H}_3 \mathrm{O}^{+}\right)+\lambda\left(\mathrm{A}^{-}\right)\right] \cdot\left[\mathrm{H}_3 \mathrm{O}^{+}\right] \quad \Rightarrow \quad\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_{\text {éq }}=\frac{\sigma_{\hat{\varepsilon q}}}{\lambda\left(\mathrm{H}_3 \mathrm{O}^{+}\right)+\lambda\left(\mathrm{A}^{-}\right)}
$$
On a : $\lambda\left(\mathrm{H}_3 \mathrm{O}^{-}\right)=35.10^{-3} \mathrm{~S} . \mathrm{m}^2 \mathrm{~mol}^{-1}, \lambda\left(A^{-}\right)=4,09.10^{-3} \mathrm{~S} \cdot \mathrm{~m}^2 \mathrm{~mol}^{-1}$
$$
\Rightarrow\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_1=8,9 \cdot 10^{-4} \mathrm{~mol} / \mathrm{L} \Rightarrow Q_{r-\varepsilon q}=1,6 \cdot 10^{-5} .
$$
2. Détermination de $Q_{r-e ́ q}$
On considère une solution aqueuse d’acide éthanoïque à la concentration $C$ connue. L’équation de la réaction est
$$
\mathrm{CH}_3 \mathrm{COOH}_{(a q)}+\mathrm{H}_2 \mathrm{O}_{(\mathrm{aq})} \leftrightharpoons \mathrm{CH}_3 \mathrm{COO}_{(\mathrm{aq})}^{-}+\mathrm{H}_3 \mathrm{O}_{(\mathrm{aq})}^{+}
$$
Dans la suite, pour rester le plus général possible, l’acide sera noté AH et sa base conjuguée (ion éthanoate) sera noté $A^{-}$.
Tableau d’avancement

On a : $\left[H_3 O^{+}\right]_{e ́ q}=\left[A^{-}\right]_{e ́ q}=\frac{\mathbf{x}_{\text {eqq }}}{\mathbf{V}}$ et $[A H]_{e_q}=C-\frac{\mathbf{x}_{\text {éq }}}{\mathbf{V}}=C-\left[H_3 O^{+}\right]_{e q q}$.
la constante d’équilibre: $\quad \mathbf{Q}_{\text {réq }}=\frac{\left[\mathrm{HCOO}^{-}\right] \cdot\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{[\mathrm{HCOOH}]}$ donc $\quad \mathbf{Q}_{\text {réq }}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]^2}{\mathrm{C}-\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}$.
ー Par conductivité
À $25^{\circ} \mathrm{C}$ on prend une solution $S_1 d^{\prime}$ acide éthanoïque de concentration $C_1=5.10^{-2} \mathrm{~mol} / \mathrm{L}$, sa conductivité est $\sigma_{e q}=34,79 \cdot 10^{-3} \mathrm{~S} . \mathrm{m}^{-1}$.
Les ions présents dans la solution sont $\mathrm{A}^{-}$et $\mathrm{H}_3 \mathrm{O}^{+}$.
la conductivité de la solution est : $\sigma_{e_q}=\lambda\left(\mathrm{H}_3 \mathrm{O}^{+}\right) \cdot\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_{\varepsilon_q}+\lambda\left(\boldsymbol{A}^{-}\right) \cdot\left[\boldsymbol{A}^{-}\right]_{e_q}$
$$
\Rightarrow \quad \sigma_{e q q}=\left[\lambda\left(H_3 O^{+}\right)+\lambda\left(A^{-}\right)\right] \cdot\left[H_3 O^{+}\right] \quad \Rightarrow \quad\left[H_3 O^{+}\right]_{\text {éq }}=\frac{\sigma_{e q}}{\lambda\left(H_3 O^{+}\right)+\lambda\left(A^{-}\right)}
$$
On a : $\lambda\left(\mathrm{H}_3 \mathrm{O}^{-}\right)=35.10^{-3} \mathrm{~S} . \mathrm{m}^2 \mathrm{~mol}^{-1}, \lambda\left(A^{-}\right)=4,09.10^{-3} \mathrm{~S} . \mathrm{m}^2 \mathrm{~mol}^{-1}$
$$
\Rightarrow\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_1=8,9.10^{-4} \mathrm{~mol} / \mathrm{L} \Rightarrow Q_{r-\hat{e}_q}=1,6.10^{-5} .
$$
ーPar PH-métrie
$\grave{A} 25^{\circ} \mathrm{C}$ on prend une solution $\mathrm{S}_2$ d’acide éthanoïque de concentration $\mathrm{C}_1=5.10^{-3} \mathrm{~mol} / \mathrm{L}$,
La mesure de son PH donne la valeur $\mathrm{pH}=3,55$
$$
\mathrm{PH}=3,55 \Rightarrow\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=2,8 \cdot 10^{-4} \mathrm{~mol} / \mathrm{L} \Rightarrow Q_{r-\varepsilon} q=1,6 \cdot 10^{-5} .
$$
3.Conclusion
D’après ce qui précède, la constante d’équilibre est indépendante de l’état initial des réactifs.
La constante d’équilibre est une constante qui caractérise l’état final d’une réaction et qui ne dépend que de la température.
$\grave{A} 25^{\circ} \mathrm{C}$
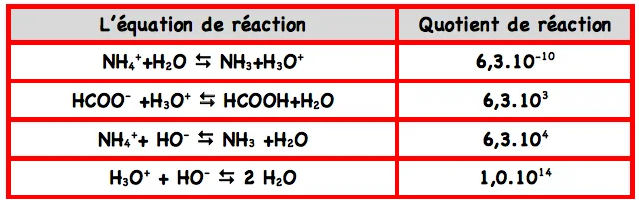
III. Influence sur le taux d'avancement.
1) Influence de la concentration initiale.
On considère la réaction suivante $\quad \mathrm{AH}+\mathrm{H}_2 \mathrm{O} \leftrightarrows \mathrm{A}^{-}+\mathrm{H}_3 \mathrm{O}^{+}$
$D^{\prime}$ après le tableau d’avancement on $a$ : $x_{\text {eq }}=\left[H_3 \mathrm{O}^{+}\right]_{\text {eq }} . V$ et $x_m=C V$.
donc le taux d’avancement final est : $\quad \tau=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_{\text {eq }}}{C}$
On prend à $25^{\circ} \mathrm{c}$ deux solutions $S_1$ et $S_2$ du même acide et de concentrations différentes
$$
\begin{array}{|c|c|c|}
\hline \text { Solution } & \mathrm{S}_1 & \mathrm{~S}_2 \\
\hline \mathrm{C} & 5.10^{-2} & 5.10^{-3} \\
\hline\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_{\text {eq }} & 8,9.10^{-4} & 2,8.10^{-4} \\
\hline \tau & 1,8 \% & 5,6 \% \\
\hline
\end{array}
$$
On a $C_1>C_2$ et $\tau_1<\tau_2$ donc $\tau$ est grand pour les solutions les moins concentrées.
2) Influence de la constante d’équilibre.
On considère, à $25^{\circ} \mathrm{c}$, deux solutions aqueuses
$\mathrm{S}_1$ et $\mathrm{S}_2$ de même concentration $\mathrm{C}=5.10^{-2} \mathrm{~mol} / \mathrm{L}$.
𓄲 $>\mathrm{S}_1$ solution d’acide éthanoïque $\mathrm{CH}_3 \mathrm{COOH}, \mathrm{PH}_1=3,05$
𓄲 $>\mathrm{S}_2$ solution d’acide méthanoïque $\mathrm{HCOOH}, \mathrm{PH}_2=2,55$
L’équation de réaction $\mathrm{AH}+\mathrm{H}_2 \mathrm{O} \leftrightarrows \mathbf{A}^{-}+\mathrm{H}_3 \mathrm{O}^{+} \quad \tau=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_{e q}}{c}$ et $\mathbf{Q}_{\text {réq }}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]^2}{\mathrm{C}-\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}$
$$
\begin{array}{|c|c|c|}
\hline \text { Solution } & S_1 & S_2 \\
\hline\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_{\text {éq }} & 8,9.10^{-4} & 2,8.10^{-3} \\
\hline Q_{\text {réq }} & 1,6.10^{-5} & 1,6.10^{-4} \\
\hline \tau & 1,8 \% & 5,6 \% \\
\hline
\end{array}
$$
On constate que pour des solutions de même concentration, le taux d’avancement à l’équilibre est d’autant plus élevé que la constante d’équilibre $K$ est plus grande.
On prépare, à $25^{\circ} \mathrm{c}$, une solution S d’acide éthanoïque de $\mathrm{pH}=3,4$ à.
Pour cela, on dissout une masse $m=0,6 \mathrm{~g}$ d’acide éthanoïque pur dans l’eau distillée pour préparer un volume $V_s=1,00 \mathrm{~L}$ de solution.
1) Écrire l’équation bilan de la réaction entre l’acide éthanoïque et l’eau.
2) Calculer la quantité de matière $n_0$ en soluté introduit dans la solution et en déduire que la concentration de la solution en soluté apporté vaut: $C=1,0.10^{-2} \mathrm{~mol} / \mathrm{L}$.
3) Dresser le tableau d’avancement de la réaction entre l’acide éthanoïque et l’eau.
4) Calculer la valeur de la constante d’équilibre de cette réaction.
5) On dilue $n$ fois la solution $S$, on obtient une solution $S^{\prime}$, la mesure de la conductivité de $S^{\prime}$ donne la valeur $\sigma=4,92 \cdot 10^{-3} \mathrm{~S} / \mathrm{m}$. Déterminer la valeur du facteur de dilution n .
Données : $M(C)=12,0 \mathrm{~g} / \mathrm{mol} ; M(H)=1,00 \mathrm{~g} / \mathrm{mol} ; M(O)=16,0 \mathrm{~g} / \mathrm{mol}$ $\lambda\left(\mathrm{H}_3 \mathrm{O}^{+}\right)=35.10^{-3} \mathrm{~S} . \mathrm{m}^2 \mathrm{~mol}^{-1}, \lambda\left(\mathrm{CH}_3 \mathrm{COO}\right)=4,09.10^{-3} \mathrm{~S} . \mathrm{m}^2 \mathrm{~mol}^{-1}$
1) On considère la réaction d’équation $A_{a q}+B_{a q} \leftrightarrows C_{a q}+D_{a q}$
a) Dans le cas où $n_0(A)=n_0(B)$, déterminer l’expression du taux d’avancement final $\tau$ en fonction de la constante d’équilibre $K$.
b) Calculer la valeur de $\tau$ pour $K=10^2$ puis pour $K=10^4$.
2) On considère l’action d’un acide AH sur l’eau.
a) Écrire l’équation de la réaction.
b) montrer que $\tau=\frac{\mathrm{K}}{\mathrm{K}+10^{-\mathrm{PH}}}$ et puis montrer que pour $\tau=50 \%$ on a $\mathrm{K}=10^{-\mathrm{PH}}$.