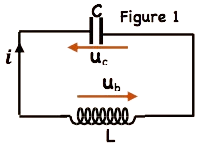Le circuit RLC libre
I. Décharge d'un condensateur dans une bobine.
1) Expérience.
Considérons le circuit suivant :
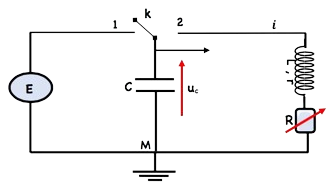
✹K est en position 1 , le condensateur se Charge, à la fin de la charge on a:
$$
u_{c \max }=E \quad, \quad q_{\max }=C \cdot E \quad \text { et } \quad \xi_{\max }=\frac{1}{2} \cdot C \cdot E^2
$$
✹À un instant $t=0$ on bascule $k$ en position 2 et on visualise la tension $u_c$ au borne du condensateur pour une $R$ résistance faible, on obtient la courbe ci-dessous.
✹$\hat{A}$ un instant $t=0$ on bascule $k$ en position 2 et on visualise la tension $u_c$ au borne du condensateur pour une $R$ résistance faible, on obtient la courbe ci-dessous.
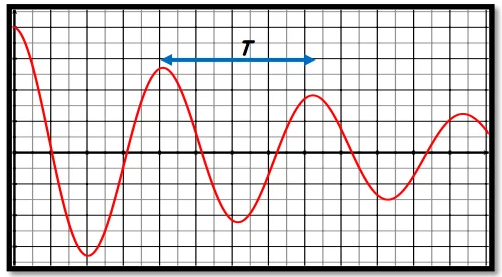
On obtient des oscillations dont l’amplitude diminue (un amortissement).
Donc le circuit RLC est le siège d’oscillation électrique libre et amortie.
2) Les régimes d’oscillation.
On enregistre la tension $u_c $ aux bornes du condensateur, pour différentes valeurs de la résistance $R_T=R+r$.
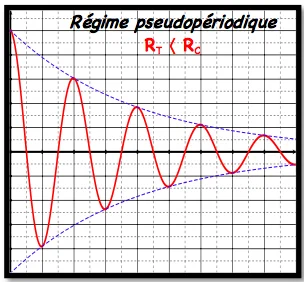
✹Si $\mathrm{R}_T$ est faible, on obtient des oscillations amorties. Le régime est dit pseudopériodique, la durée $T$ est la pseudopériode.
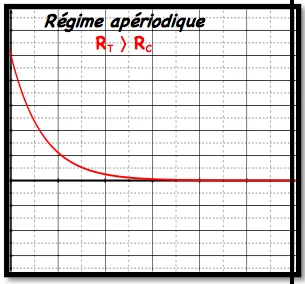
✹Si $R$ est élevée, il n’y a plus d’oscillations. Le régime est dit apériodique.
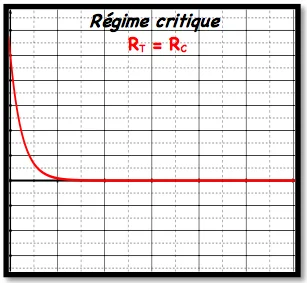
La valeur de la résistance correspondant au passage du régime pseudopériodique au régime apériodique est appelée résistance critique $R_c$; sa valeur dépend de $L$ et de $C$. donc pour $R=R_c$ on obtient un régime critique.
La courbe de la tension du condensateur selon la valeur de la résistance du circuit :
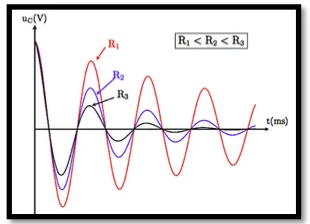
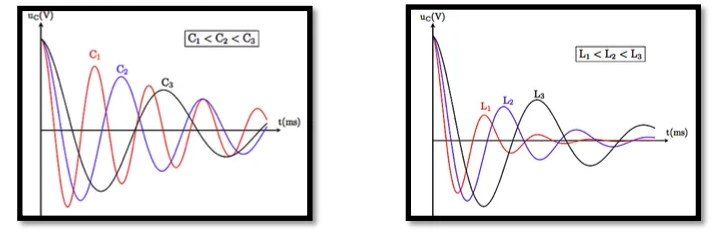
Influence des paramètres du circuit
•L’influence de la résistance
• L’influence de la capacité ou de l’inductance
II. Décharge d'un condensateur dans une bobine idéale (LC).
1) Équation différentielle.
La loi d’additivité des tensions: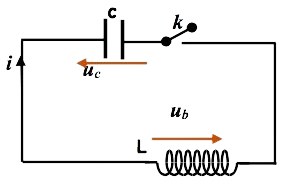
$u_c+u_b=0 \Rightarrow u_c+L \cdot \frac{d i}{d t}=0$
$$
\begin{array}{ll}
\Rightarrow & u_c+L C \cdot \frac{d^2 u_c}{d t^2}=0 \\
\Rightarrow & \quad \frac{d^2 u_c}{d t^2}+\frac{1}{L C} \cdot u_c=0
\end{array}
$$
2) Ia solution de l’équation différentielle.
La solution générale de l’équation différentielle précédente est de la forme :
$$
u_c(t)=A \cdot \cos \left(\omega_0 t+\varphi\right)
$$
avec:
$\omega_0$ la pulsation propre du circuit, $\omega_0=\frac{2 \pi}{T_0}$ (en : rad $/ \mathrm{s}$ ).
$\mathrm{T}_0$ : période propre des oscillations. (en : s)
A : amplitude, $c^{\prime}$ est la tension maximum $A=u_{c \max }=E$.
$\varphi$ : c’est la phase initiale ( à $t=0$ ), c’est une constante qui dépend des conditions initiales. (en: rad) $(-\pi<\varphi \leq \pi)$
a) Détermination de la période propre :
$$
\begin{aligned}
\text { on } a: u_c(t)=A \cdot \cos \left(\omega_0 t+\varphi\right) & \Rightarrow \frac{d^2 u_c}{d t^2}=-\left(\frac{2 \pi}{T_0}\right)^2 \cdot U_{C \max } \cdot \cos \left(\frac{2 \pi}{T_0} t+\varphi\right) \\
& \Rightarrow \frac{d^2 u_c}{d t^2}=-\left(\frac{2 \pi}{T_0}\right)^2 \cdot u_c(t) \Rightarrow \frac{d^2 u_c}{d t^2}+\left(\frac{2 \pi}{T_0}\right)^2 \cdot u_c(t)=0
\end{aligned}
$$
par identification avec l’équation différentielle, on $a:\left(\frac{2 \pi}{T_0}\right)^2=\frac{1}{L C} \quad \Rightarrow \quad T_0=2 \pi \cdot \sqrt{L C}$
b) Détermination de la phase:
$\grave{A} t=0$ on $a u_c=U_{\text {cmax }} \Rightarrow \cos (\varphi)=1 \Rightarrow \varphi=0$.
Donc $\quad: u_c(t)=E \cdot \cos \left(\frac{2 \pi}{T_0} t\right)$
3) L’intensité du courant $i(t)$.
$$
\begin{aligned}
& \left.\begin{array}{cc}
\text { on a } & u_c(t)=E \cdot \cos \left(\frac{2 \pi}{T_0} t\right) \\
\text { et } & i(t)=C \frac{d u_c}{d t}
\end{array}\right\} i(t)=-C E \frac{2 \pi}{T_0} \sin \left(\frac{2 \pi}{T_0} t\right) \quad \text { d’où } \quad i(t)=-E \sqrt{\frac{C}{L}} \sin \left(\frac{2 \pi}{T_0} t\right) \\
& -1 \leq \sin \left(\frac{2 \pi}{T_0} \cdot t\right) \leq 1 \quad \Rightarrow \quad-E \sqrt{\frac{C}{L}} \leq i(t) \leq E \sqrt{\frac{c}{L}} \quad \Rightarrow \quad \mathrm{I}_{\max }=\mathrm{E} \sqrt{\frac{C}{L}} \\
& \text { Donc : } i(t)=-\mathrm{I}_{\mathrm{m}} \sin \left(\frac{2 \pi}{T_0} t\right)
\end{aligned}
$$
$$
\begin{array}{|c|c|c|c|c|c|}
\hline t & 0 & T_0 / 4 & T_0 / 2 & 3 T_0 / 4 & \mathrm{~T}_0 \\
\hline \mathrm{u}_{\mathrm{c}}(t) & \mathbf{E} & 0 & -\mathrm{E} & 0 & \mathbf{E} \\
\hline i(t) & 0 & -\mathrm{I}_{\mathrm{m}} & 0 & \mathrm{I}_{\mathrm{m}} & \mathbf{0} \\
\hline
\end{array}
$$
4) Étude énergétique.
a) L’énergie électrique:
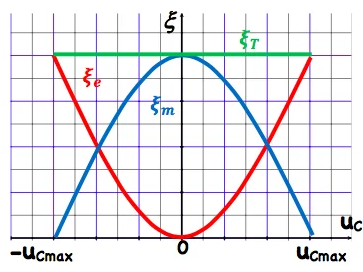
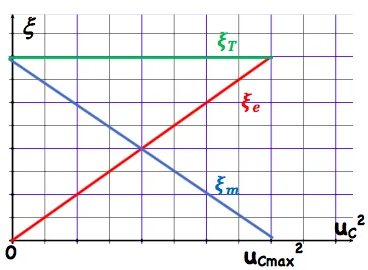
L’énergie emmagasinée par le condensateur à un instant t est : $\quad \xi_e(t)=\frac{1}{2} C . u_c^2$
$$
\begin{array}{r}
\Rightarrow \quad \xi_e(t)=\frac{1}{2} C \cdot U_{C \max }^2 \cos ^2\left(\frac{2 \pi}{T_0} t\right) \text { et on a } \xi_{e-\max }=\frac{1}{2} C \cdot U_{C \max }^2 \\
\text { donc } \xi_e(t)=\xi_{e-\max } \cdot \cos ^2\left(\frac{2 \pi}{T_0} t\right)
\end{array}
$$
b) L’énergie magnétique
L’énergie emmagasinée par la bobine à un instant $t$ est : $\quad \xi_m(t)=\frac{1}{2} L . i^2$
$$
\begin{aligned}
& \Rightarrow \quad \xi_m(t)=\frac{1}{2} L \cdot I_{\max }^2 \sin ^2\left(\frac{2 \pi}{T_0} t\right) \quad \text { et on a } \xi_{m-\max }=\frac{1}{2} L \cdot I_{\max }^2=\frac{1}{2} L \cdot\left(E \sqrt{\frac{C}{L}}\right)^2=\frac{1}{2} C \cdot U_{C \max }^2 \\
& \text { donc } \quad \xi_{e-\max }=\xi_{m-\max }=\xi_{\max } \text { et } \quad \xi_m(t)=\xi_{\max } \cdot \sin ^2\left(\frac{2 \pi}{T_0} t\right)
\end{aligned}
$$
c) L’énergie totale
L’énergie emmagasinée dans le circuit est: $\xi_T=\xi_e(t)+\xi_m(t)$
$$
\begin{aligned}
\Rightarrow \quad \xi_{\mathrm{T}}=\xi_{\max } \cdot \cos ^2\left(\frac{2 \pi}{T_0} t\right)+\xi_{\max } \cdot \sin ^2\left(\frac{2 \pi}{T_0} t\right) & \Rightarrow \xi_{\mathrm{T}}=\xi_{\max }=\xi_{\max } \\
& \Rightarrow \xi_{\mathrm{T}}=\frac{1}{2} C \cdot U_{C \max }^2=\frac{1}{2} L \cdot I_{\max }^2
\end{aligned}
$$
l’énergie total du circuit LC se conserve.
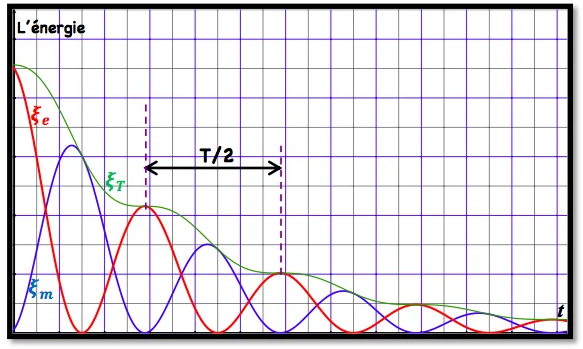
Remarques
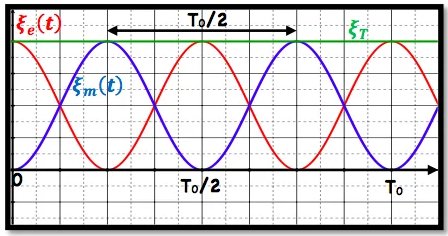
⊹ La période de la variation de l’énergie
$$
\begin{array}{|c|c|c|c|c|c|}
\hline \mathbf{t} & 0 & T_0 / 4 & T_0 / 2 & 3 T_0 / 4 & T_0 \\
\hline \xi_e(\boldsymbol{t}) & \xi_{\max } & 0 & \xi_{\max } & 0 & \xi_{\max } \\
\hline \boldsymbol{\xi}_m(\boldsymbol{t}) & 0 & \xi_{\max } & 0 & \xi_{\max } & 0 \\
\hline
\end{array}
$$
$$
\text { La période des variations de l’énergie est la moitié de la période propre. }
$$
⊹ La conservation de l’énergie totale
$$
\begin{array}{rlll}
\xi_T=\frac{1}{2} C u_c^2+\frac{1}{2} L i^2 \quad \Rightarrow & \frac{d \xi_T}{d t}=C \cdot u_c \cdot \frac{d u_c}{d t}+L \cdot i \cdot \frac{d i}{d t} \quad \Rightarrow \quad \frac{d \xi_T}{d t}=u_c \cdot i+u_b \cdot \boldsymbol{i} \\
\Rightarrow \quad \frac{d \xi_T}{d t}=\left(u_c+u_b\right) \cdot i & \Rightarrow \quad \frac{d \xi_T}{d t}=0 \quad \Rightarrow \quad \xi_T=\text { Cte }
\end{array}
$$
$$
\xi=f\left(u_c\right)
$$
$$
$$
\xi=f\left(u_c{ }^2\right)
$$
III. Influence de la résistance $R$ sur les oscillations (RLC).
1) L’équation différentielle.
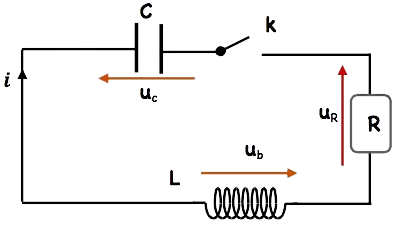
La loi d’additivité des tensions:
$$
u_c+u_b+u_R=0
$$
avec : $\quad u_R=R . i=R C \frac{d u_C}{d t} \quad$ et $\quad u_b=r . i+L \cdot \frac{d i}{d t}=r C \cdot \frac{d u_C}{d t}+L C \cdot \frac{d^2 u_C}{d t^2}$.
donc : $u_C+(R+r) \cdot C \frac{d u_C}{d t}+L C \cdot \frac{d^2 u_C}{d t^2}=0 \quad \Rightarrow \quad \frac{d^2 u_C}{d t^2}+\left(\frac{R+r}{L}\right) \frac{d u_C}{d t}+\frac{1}{L C} \cdot u_C=0$.
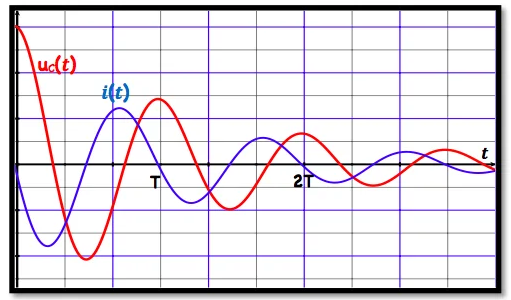
en régime pseudopériodique, la tension $u_c(t)$ et l’intensité $i(t)$ varient de la façon suivante:
2) Étude énergétique.
L’énergie totale emmagasinée dans la circuit RLC est: $\boldsymbol{\xi}_{\mathrm{T}}=\frac{1}{2} \mathrm{Cu}_{\mathrm{c}}^2+\frac{1}{2} \mathrm{~L} i^2$
Donc $\frac{d \xi_T}{d t}=C . u_c \cdot \frac{d u_c}{d t}+$ L.i. $\frac{d i}{d t} \quad \Rightarrow \frac{d \xi_T}{d t}=u_c, i+u_b, i$
$\Rightarrow \frac{d \xi_T}{d t}=\left(u_c+u_b\right) \cdot i$, et on a d’après la loi d’additivité des tensions: $\mathbf{u}_c+\mathrm{L} \cdot \frac{d i}{d t}=-(\mathrm{R}+\mathrm{r}) \cdot \boldsymbol{i}$
$$
\text { donc } \frac{d \xi_T}{d t}=-(R+r) i^2 \Rightarrow \frac{d \xi_T}{d t}<0
$$
$\xi_{\mathrm{T}}$ diminue au cours du temps par effet joule
Remarques
ー L’énergie dissipée entre deux instant $t_1$ et $t_2$ est : $\xi_{\text {th }}=\xi_T\left(t_1\right)-\xi_T\left(t_2\right)$.
ー En régime pseudo périodique :
$\checkmark$ Pour $u_c= \pm U_{\max }$ on $a i=0$, donc $\xi_T=\xi_{\text {emax }}=\frac{1}{2} C . u_{c \max }^2$
$\checkmark$ Pour $i= \pm I_{\max }$ on $a \frac{d i}{d t}=0$ donc $u_b= \pm r \cdot I_{\max }$ et $u_c= \pm(r+R) \cdot I_{\max }$
Ce qui donne $\xi_{\mathrm{m}}=\xi_{\text {mmax }}$ et $\xi_{\mathrm{e}}=\frac{1}{2} C(R+r)^2 I_m^2$
donc $\xi_{\mathrm{T}}=\frac{1}{2} L \cdot I_{\max }^2+\frac{1}{2} C(R+r)^2 I_m^2=\frac{1}{2} \cdot I_{\max }^2\left[\mathrm{~L} .+C(R+r)^2\right]$
3) L’entretien des oscillations amorties
La résistance est responsable de l’amortissement des oscillations; elle consomme de l’énergie sous forme d’effet joule. Pour que les oscillations soient sinusoïdales, il faut compenser cette énergie perdue et cela en utilisant un générateur d’entretien. La loi $d^{\prime}$ additivité des tensions: $U_G=U_C+U_b+U_R \Rightarrow U_G=U_C+r i+L_i \frac{d i}{d t}+R i$
$$ \Rightarrow u_G=u_C+R_T i+L C \frac{d^2 u_C}{d t^2} $$
pour avoir des oscillation entretenues il faut que : $u_c+L C \frac{d^2 u_C}{d t^2}=0$ donc
$$ u_G=(R+r) \cdot i $$
Remarque : Le générateur $G$ compense l’énergie perdue donc sa puissance est : $\mathcal{P}_G=R_T i^2$ et on a $\mathcal{P}_G=u_G . i$ donc $u_G=R_T i$.
Un condensateur de capacité $C$ initialement chargé, est branché avec une bobine d’inductance $L$ et de résistance négligeable.
À l’aide d’un oscilloscope, on visualise la tension $u_c(\dagger)$ aux bornes du condensateur
1-Établir l’équation différentielle vérifiée par $u_c(t)$.
2-En déduire l’expression de la tension $u_c(\dagger)$ en fonction des paramètre du circuit.
3-Exprimer l’intensité du courant en fonction du temps.
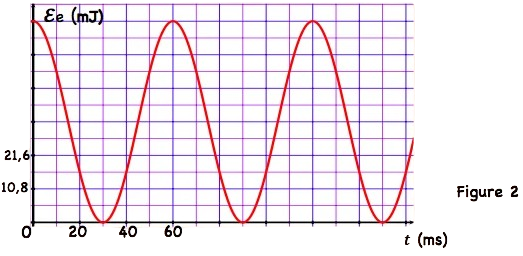
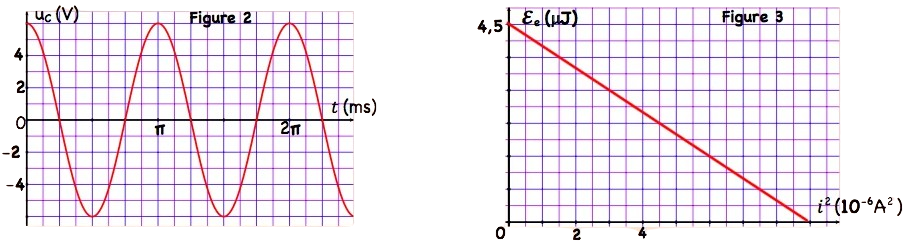
4-Une étude expérimentale nous permet de tracer la courbe qui représente la variation de l’énergie électrique $\mathrm{E}_e$ emmagasinée dans le condensateur en fonction de $i^2$ (figure 3 ).
4-1-Montrer que l’énergie totale $\mathcal{E}_{\text {T }}$ se conserve au cours du temps.
4-2-Déterminer l’expression de l’énergie globale $\mathcal{E}_{\mathrm{T}}$ en fonction de $i^2$ et d’autre paramètres du circuit.
4-3-justifier la forme de la courbe de la figure 3.
5 –En utilisant les figure 2 et 3 , déterminer les valeurs de $I_m, L, C$ et $Q_m$.
On réalise le circuit représenté sur la figure 1 qui est constitué de :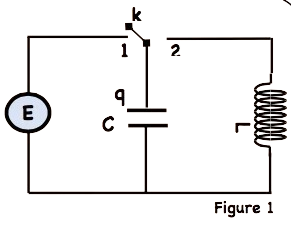
– Un générateur de tension de f.e.m $E$ et de résistance interne négligeable.
– Un condensateur de capacité $C=9.10^{-4} \mathrm{~F}$.
– Une bobine d’inductance $L$ et de résistance $r$.
– Un interrupteur K à double position.
On met l’interrupteur à la position 1 jusqu’à ce que le condensateur soit chargé totalement et on le bascule vers la position 2 à l’instant $t=0$.
1- Établir l’équation différentielle vérifiée par la charge q du condensateur.
2-Déterminer l’expression de la période propre $T_0$ pour que l’expression $q(t)=Q_m \cos \left(\frac{2 \pi}{T_0} . t\right)$ soit solution de l’équation différentielle.
3-Vérifier que $\mathrm{T}_0$ a une dimension temporelle.
4-Montrer que l’énergie électrique $\mathcal{E}_e s^{\prime}$ écrit de la forme suivante $\mathcal{E}_e(t)=\frac{1}{4} \cdot C \cdot E^2\left(1-\cos \left(\frac{4 \pi}{T_0} \cdot t\right)\right)$.
5-La figure 2 donne les variations de l’énergie électrique $\varepsilon_e$ en fonction du temps.
5-1 Déterminer la valeur de To.
5-2 En déduire la valeur de l’inductance de la bobine utilisée.
5-3 Déterminer la valeur de f.e.m $E$ du générateur et déduire la valeur de $Q_m$.
