Le circuit RL
I. La bobine
Une bobine est constituée d’un enroulement cylindrique d’un fil conducteur de résistance r, recouvert d’un isolant.
II. Influence d'une bobine dans un circuit.
1-Expérience :
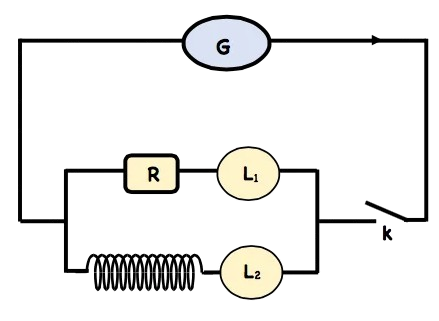
On considère le montage suivant formé de deux lampes identiques, un résistance $R$, une bobine de résistance interne $r=R$ et un générateur de tension de f.e.m $E$.
On ferme l’interrupteur $k$ et on observe que La lampe $L_2$ s’allume avec un retard par rapport à la lampe $L_i$, et puis les deux lampes s’allument de la même façon.
2- consequence
On constate qu’il se produit un retard à l’établissement du courant dans la portion de circuit qui comporte la bobine,
donc
Une bobine s’oppose transitoirement à l’établissement du courant dans un circuit. En régime permanent, la bobine se comporte comme un conducteur ohmique de résistance $r$
III. La tension au borne d'une bobine
1) Expérience 1
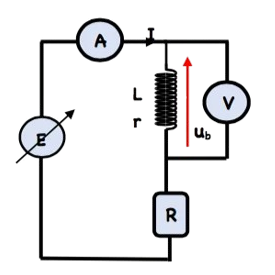
On considère le montage suivant formé d’une bobine, une résistance $R$ et un générateur de f.e.m $E$ réglable. On fait varier la valeur de $E$ et on note la valeur de I passant par la bobine et la tension $U_b$ entre ses bornes.
$$
\begin{array}{|c|c|c|c|c|c|}
\hline \mathrm{u}_{\mathrm{b}}(V) & 0 & 1 & 2 & 3 & 4 \\
\hline I \quad(A) & 0 & 0,08 & 0,16 & 0,24 & 0,32 \\
\hline U / I(\Omega) & & 12,5 & 12,5 & 12,5 & 12,5 \\
\hline
\end{array}
$$
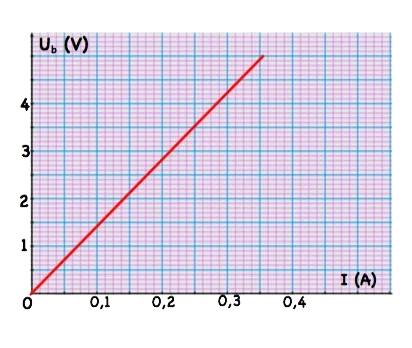
On constate que $u_b$ est proportionnel à l’intensité
I, donc:
$$
U_b=r . I
$$
$r$ est la résistance interne de la bobine
la bobine se comporte comme une résistance lorsqu’elle est parcourue par un courant continue.
2) Expérience 2
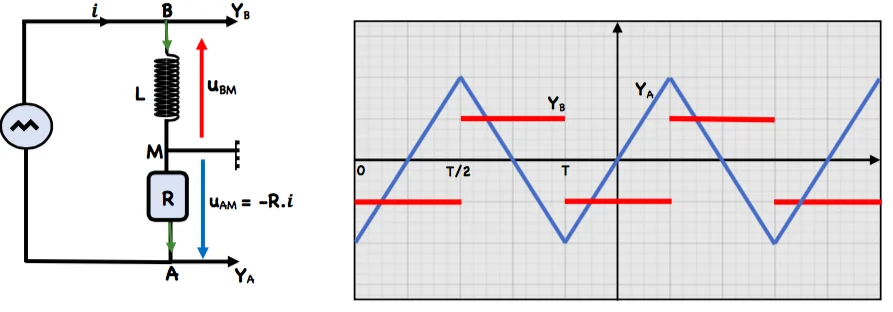
On change le générateur précédent par un GBF délivrant une tension triangulaire et on néglige la résistance de la bobine devant celle du résistor.
On visualise la tension $u_{s M}$ au borne de la bobine et la tension $u_{A M}$ au borne de la résistance.
$$
\begin{array}{|c|c|c|c|c|}
\hline \text { L’intrval } & \text { U }_{A M}=-R . i & i & \frac{d i}{d t} & \text { u }_{B M} \\
\hline\left[0-\frac{T}{2}[ \right. & a . t+b & -\frac{a}{R} \cdot t-\frac{b}{R} & -\frac{a}{R}=\text { Cte }\langle 0 & -k=\text { Cte }\langle 0 \\
\hline\left[\frac{T}{2}-T[ \right. & -a . t+b^{\prime} & \frac{a}{R} \cdot t-\frac{b^{\prime}}{R} & \left.\frac{a}{R}=\text { Cte }\right\rangle 0 & k=\text { Cte }\rangle 0 \\
\hline
\end{array}
$$
En faisant varier le coefficient $a$ on constate que $u_b$ varie proportionnellement donc $u_{B M}$ est proportionnelle à $\frac{d i}{d t}$, le facteur de proportionnalité est appelé coefficient d’auto-induction de la bobine, on le noté L, son unité est le Henry (H)
L représente le pouvoir de s’opposer à la variation du courant dans ses spires, il dépond des propriétés de la bobine
$$
u_b(t)=L \frac{d i(t)}{d t}
$$
3) la tension au borne d’une bobine.
En convention récepteur on a pour une bobine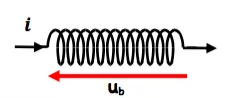
de résistance $r$ et d’induction $L$.
$$
u_b(t)=r . i+L \frac{d i(t)}{d t}
$$
IV. Réponse d'un dipôle RL à un échelon de tension
1) le montage du circuit.
$k$ fermé ,la tension $u_{A B}$ est $E$ (échelon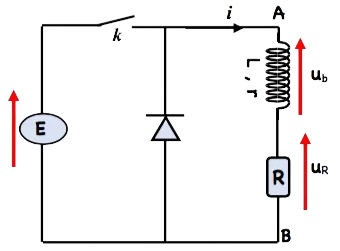
ascendant)
$k$ ouvert , la tension $u_{A B} s^{\prime}$ annule (échelon descendant)
2) L’établissement de courant.
À un instant $t=0$ on ferme $k$, la diode bloque le courant.
a) Équation différentielle vérifiée par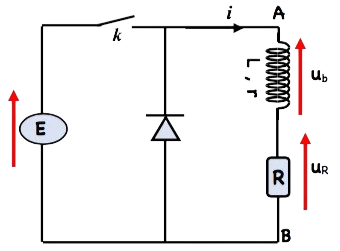
le courant $i$.
La loi d’additivité des tensions appliquée aux bornes du dipôle RL permet d’écrire:
$$
u_{\mathrm{R}}+u_{\mathrm{b}}=\mathrm{E} \quad \Rightarrow \mathrm{Ri}+\mathrm{ri}+\mathrm{L} \frac{d i}{d t}=\mathrm{E}
$$
Finalement l’équation différentielle cherchée s’écrit
$$
\frac{L}{R+r} \cdot \frac{d i}{d t}+i=\frac{E}{R+r}
$$
b) solutions d’équation différentielle.
La solution générale de l’équation différentielle précédente est $i(t)=A . e^{-t / \tau}+B$ A, B et $\tau$ sont des constantes à déterminer.
Pour déterminer les constantes $A, B$ et $\tau$ il faut suivre les étapes suivantes:
$>$ On remplace la solution dans l’équation différentielle
Donc : $\frac{L}{R+r} \cdot \underbrace{\left(A \cdot \frac{-1}{\tau} e^{-t / \tau}\right.}_{\frac{d i}{d t}})+\underbrace{A \cdot e^{-t / \tau}+B}_i=\frac{E}{R+r} \Rightarrow\left(1-\frac{L}{R+r} \cdot \frac{1}{\tau}\right) \cdot A e^{-t / \tau}=\frac{E}{R+r}-B$.
Pour que cet équation soit vérifié $\forall t$ il faut que : $\Rightarrow \underbrace{(\underbrace{1-\frac{L}{R+r} \cdot \frac{1}{\tau}})}_{=0} \cdot A e^{-+/ \tau}=\underbrace{\frac{E}{R+r}-\mathrm{B}}_{=0}$
Donc
$$
\tau=\frac{L}{R+r} \text { et } \mathrm{B}=\frac{E}{R+r} \text {. }
$$
$$
\begin{aligned}
&\text { Les conditions initiales : à } t=0 \text { on a } i=0 \text { (la bobine empêche le courant de passer) donc }\\
&A+B=0 \quad \Rightarrow \quad A=-B=-\frac{E}{R+r}
\end{aligned}
$$
$$
\begin{aligned}
&\text { On pose } \mathrm{Ip}=\frac{E}{R+r} \quad \text { l’intensité du courant en régime permanant, donc : }\\
&i(t)=I_p \cdot\left(1-e^{-t / \tau}\right)
\end{aligned}
$$
Remarques
• $$
\begin{aligned}
\tau=\frac{L}{R_T} & \Rightarrow[\tau]=[\mathrm{L}] \cdot[\mathrm{R}]^{-1} \Rightarrow \quad[\tau]=[\mathrm{u}] \cdot[\mathrm{T}] \cdot[\mathrm{I}]^{-1} \cdot[\mathrm{U}] \cdot[\mathrm{I}]^{-1}=[\mathrm{T}]=\mathrm{s} \\
& \tau \text { est la constante du temps du circuit. }
\end{aligned}
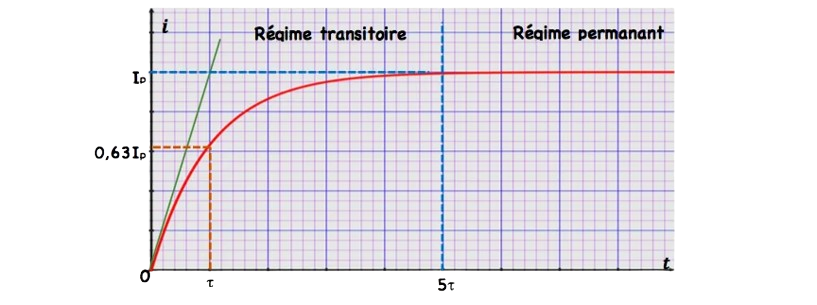
$$
• $i(\tau)=\operatorname{Ip} .\left(1-e^{-1}\right) \quad \Rightarrow \quad i(\tau)=63 \% \cdot I_p \quad$ donc $:$
$\tau$ est la durée au bout de laquelle le courant est établie à $63 \%$.
$$
\tau \text { est l’abscisse du point d’intersection de la tangente à la courbe à } t=0 \text { et la tangente à l’m. }
$$
• $$
\tau \text { est l’abscisse du point d’intersection de la tangente à la courbe à } t=0 \text { et la tangente à l’m. }
$$
• $i(5 \tau)=E .\left(1-e^{-5}\right) \Rightarrow \quad i(\tau)=99,4 \% I_p$ donc au bout de $5 \tau$ on peut considérer que le courant permanant Ip est établie.
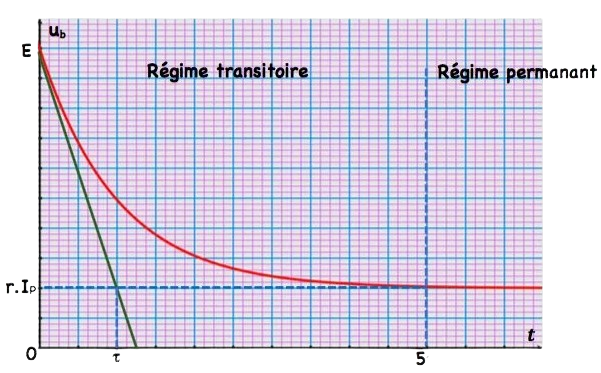
c) la tension au borne de la bobine
$$
\begin{aligned}
u_b(t)=r \cdot i+L \cdot \frac{d i}{d t} & \Rightarrow u_b(t)=r \cdot I_p \cdot\left(1-e^{-t / \tau}\right)+L \cdot I_p \cdot \frac{e^{-t / \tau} \tau}{\tau} \\
& \Rightarrow u_b(t)=r \cdot I_p \cdot\left(1-e^{-t / \tau}\right)+I_p \cdot(R+r) \cdot e^{-t / \tau} \quad \Rightarrow u_b(t)=r \cdot I_p+R \cdot I_p \cdot e^{-t / \tau}
\end{aligned}
$$
Autre méthode : $u_b(t)=E-R . i \Rightarrow u_b(t)=E-R . I_p .\left(1-e^{-t / \tau}\right) \quad \Rightarrow u_b(t)=$ r.I $I_p+$ R.I $I_p . e^{-t / \tau}$
$$
\text { donc } u_b(0)=E \text { et } u_b(\infty)=r . I_p \text {. }
$$
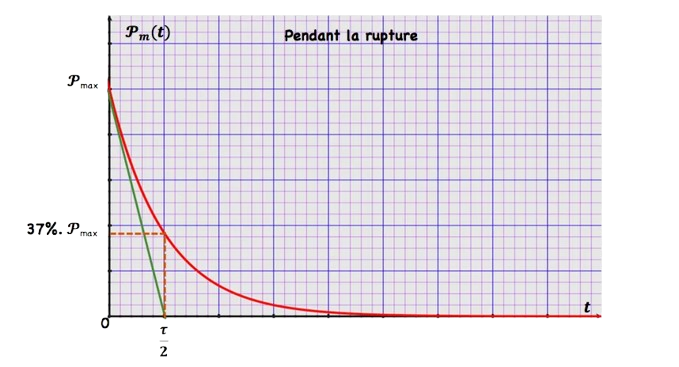
3) Rupture de courant
À un instant $t=0$ on ouvre $k$, la diode est passante et $u_D=0$
a) Équation différentielle vérifiée par le courant $i$.
La loi d’additivité des tensions appliquée aux bornes du dipôle RL permet d’écrire: $u_R+u_b=0 \Rightarrow R i+r i+L \frac{d i}{d t}=0$.
$$
\Rightarrow \quad \frac{L}{R+r} \cdot \frac{d i}{d t}+i=0
$$
b) solution d’équation différentielle.
La solution générale de l’équation différentielle précédente est $i(\dagger)=A \cdot e^{-t / \tau}+B$
$A, B$ et $\tau$ sont des constantes à déterminer.
Pour déterminer les constantes A, B et $\tau$ il faut suivre les étapes suivantes:
On remplace la solution dans l’équation différentielle
Donc : $\frac{L}{R+r} \cdot \underbrace{\left(A \cdot \frac{-1}{\tau} e^{-t / \tau}\right.}_{\frac{d i}{d t}})+\underbrace{A \cdot e^{-t / \tau}+B}_i=\frac{E}{R+r} \Rightarrow\left(1-\frac{L}{R+r} \cdot \frac{1}{\tau}\right) \cdot A e^{-t / \tau}=\frac{E}{R+r}-B$.
Pour que cet équation soit vérifié $\forall t$ il faut que : $\Rightarrow(\underbrace{\left(1-\frac{L}{R+r} \cdot \frac{1}{\tau}\right)}_{=0}) \cdot A e^{-t / \tau}=\underbrace{\frac{E}{R+r}-B}_{=0}$
Donc
$$
\tau=\frac{L}{R+r} \text { et } \mathrm{B}=\frac{E}{R+r} .
$$
$$
\begin{aligned}
&\text { Les conditions initiales : à } t=0 \text { on a } i=0 \text { (la bobine empêche le courant de passer) donc }\\
&A+B=0 \quad \Rightarrow \quad A=-B=-\frac{E}{R+r}
\end{aligned}
$$
$$
\text { donc } \quad i(t)=I_p \cdot e^{-t / \tau}
$$
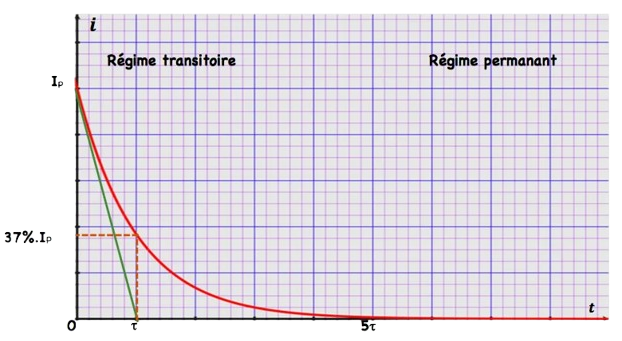
Remarques
•$$
\begin{aligned}
\mathrm{i}(\tau)=\mathrm{I}_{\mathrm{p}} \cdot \mathrm{e}^{-1} & \Rightarrow \mathrm{i}(\tau)=37 \% \mathrm{I}_p \text { donc } \\
& \tau \text { est la durée au bout laquelle le courant est rompue à } 63 \% .
\end{aligned}
$$
• $\tau$ est l’abscisse du point d’intersection de la tangente à la courbe à $t=0$ et la tangente à l’ $\infty$. $i(5 \tau)=I_p e^{-5} \approx 0$ donc au bout de $5 \tau$ on peut considérer que le courant est Rompu totalement.
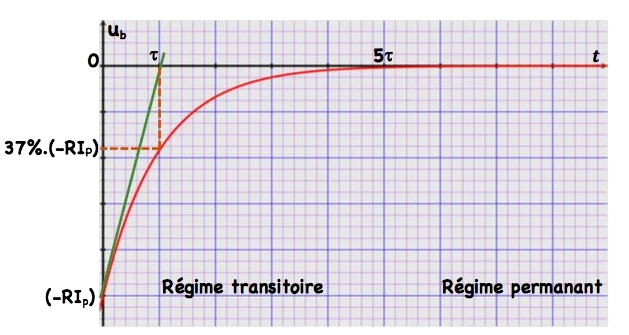
c) la tension au borne de la bobine
On $a: u_b(t)+u_R(t)=0 \Rightarrow u_b(t)=-u_R(t)=-R . i(t) \Rightarrow u_b(t)=-R \cdot I_p e^{-t / \tau}$ donc $u_b(0)=-R I_p$ et $u_b(\infty)=0$.
En absence de diode on obtient une rupture instantané de courant ce qui provoque une étincelle au niveau de l’interrupteur. C’est la surtension. Donc la diode évite la surtension.
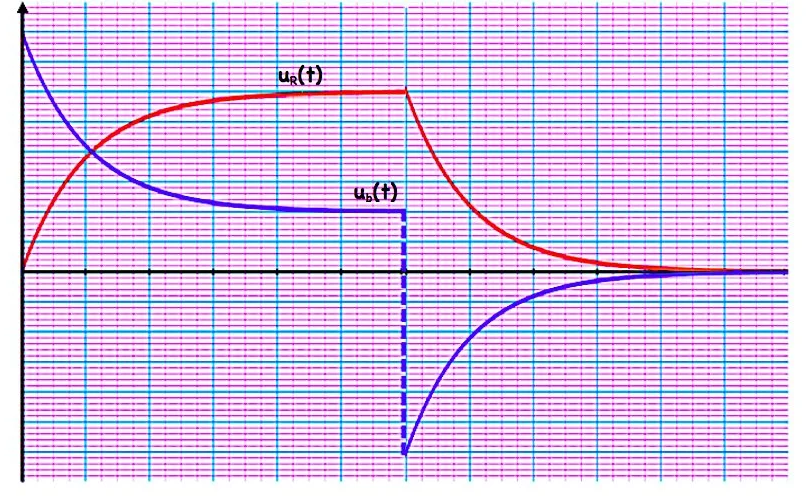
Le courant traversant la bobine est une fonction continue en fonction du temps et la tension au borne de la bobine est discontinue.
V. Énergie emmagasinée dans une bobine
1. Puissance électrique de la bobine.
$$
\begin{aligned}
&\text { La puissance instantanée reçue par la bobine est }\\
&\begin{aligned}
& P=u_b \cdot i \Rightarrow P=r \cdot i^2+L . i \cdot \frac{d i}{d t} \\
& \Rightarrow P=r \cdot i^2+\frac{1}{2} \cdot L \cdot \frac{d i^2}{d t} \\
& \Rightarrow P=r . i^2+\frac{d\left(\frac{1}{2} L i^2\right)}{d t}
\end{aligned}
\end{aligned}
$$
2. l’énergie électrique emmagasinée dans le condensateur
$\xi_e(t)$ est L’énergie reçue par la bobine. on a $P=P_{t h}+P_m$ avec $P_m=\frac{d\left(\xi_m\right)}{d t}$
$\xi_m$ est l’énergie magnétique emmagasiné par la bobine, donc $\boldsymbol{\xi}_m=\frac{1}{2} \boldsymbol{L} \boldsymbol{i}^2+$ Cte.
Pour $\mathrm{i}=0$ on $a \xi_m=0$ donc $\quad \xi_m=\frac{1}{2} L . \boldsymbol{i}^2$
Donc
$$
\begin{array}{|c|c|}
\hline \text { Pendant l’établissement } & \text { Pendant la rupture } \\
\hline \xi_e(t)=\frac{1}{2} L \cdot I_P^2\left[1-e^{-t / \tau}\right]^2 & \xi_e(t)=\frac{1}{2} L \cdot I_P^2 e^{-2 t / \tau} \\
\hline
\end{array}
$$
Exercice
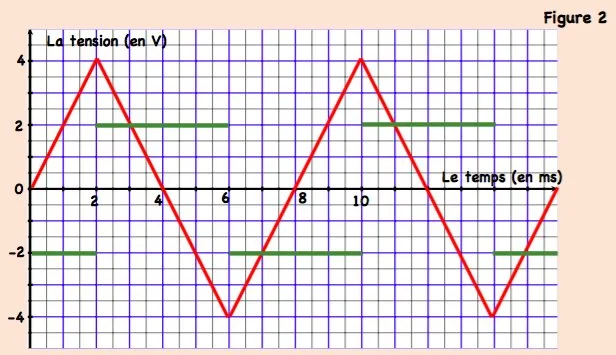
Un générateur basse fréquence (GBF) applique une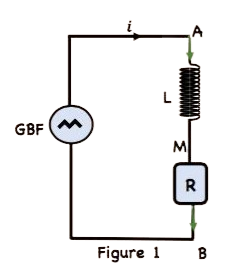 
tension alternative triangulaire aux bornes d’un dipôle $A B$ constitué d’une bobine d’inductance $L$ et de résistance négligeable et d’un conducteur ohmique de résistance $R=500 \Omega$ montés tous en série, comme le montre la figure 1. Un oscilloscope, convenablement branché, permet de visualiser, simultanément la tension $U_{A M}$ aux bornes de la bobine sur la voie $Y_1$ et la tension $u_{s M} a u x$ bornes du conducteur ohmique sur la voie $Y_2$. Les chronogrammes de la figure 2, représentent les tensions observées sur l’écran de l’oscilloscope pour une fréquence $N$ du GBF.
1-a-Identifier, parmi les chronogrammes et de la figure 3 celui qui correspond à la tension visualisée sur la voie $Y_2$. Justifier la réponse.
b- Déterminer la fréquence N du GBF.
2- Donner les expressions des tensions $u_{M M}$ et $u_{g M}$ en fonction de l’intensité $i$ du courant et des caractéristiques du dipôle $A B$.
3-a- Exprimer $u_{A M}$ en fonction de $u_{B M}$, $L$ et $R$.
b- Justifier, sur une demi-période, la forme de la tension $u_{M M}$ observée sur la voie $Y_1$.
c- Déterminer la valeur de I ‘inductance $L$ de la bobine.
Exercice
On réalise un circuit électrique AM comportant en série un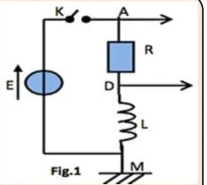
conducteur ohmique de résistance $R_0=60 \Omega$, une bobine ( $B_1$ ) d’inductance $L_1$ et de résistance supposée nulle et un interrupteur $K$. le circuit AM est alimenté par générateur de tension de fém $\mathbf{E}$ (figure-1).
Un système d’acquisition adéquat permet de suivre l’évolution au cours du temps des tensions $u_{A M}(t)$ et $u_{D M}(t)$ sont celles de la figure 2.
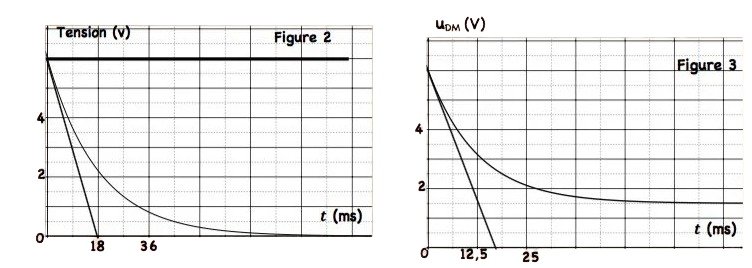
1a. Montrer que la courbe 1 correspond à $u_{D M}(t)$.
b. Donner la valeur du fém. E du générateur.
2. a. A l’instant $t_1=12 \mathrm{~ms}$, déterminer graphiquement la valeur de la tension $u_{31}$ aux bornes de l bobine ( $B_1$ ) et déduire la valeur de la tension $u_R$ aux bornes du conducteur ohmique.
b. A l’instant $t_2=108 \mathrm{~ms}$, montrer que l’intensité du courant qui s’établit dans le circuit est $I_0=0,1 \mathrm{~A}$.
3. a. Déterminer graphiquement la valeur de la constante de temps $\tau$ du dipôle RL.
b. En déduire la valeur de l’inductance $L_1$ de la bobine ( $B_1$ ).
c. Calculer l’énergie emmagasinée dans la bobine ( $B_1$ ) en régime permanant.
4. On remplace la bobine ( $B_1$ ) par une bobine ( $B_2$ ) d’inductance $L_2$ et de résistance $r$. La courbe de variation de la tension $u_{D M}(t)$ est représentée sur la figure 3.
a. Montrer qu’en régime permanant, la tension aux bornes de la bobine ( $B_2$ ) est : $u_{B 2}=r \cdot E /(r+R)$
b. Déduire la valeur de la résistance $r$ de la bobine.
c. Déterminer la valeur de l’inductance $L_2$.