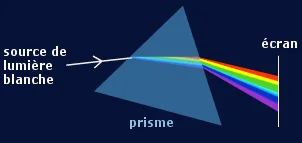
Ondes lumineuses.
I. La nature ondulatoire de la lumière
1) Expérience
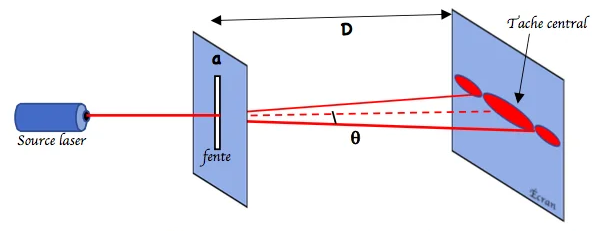
On dirige un laser rouge vers un écran. On observe sur l’écran, une tache ponctuelle rouge. On interpose alors entre la source et l’écran, une plaque percée d’une fine fente verticale.
On observe un étalement de la lumière rouge, perpendiculairement à la fente : plusieurs taches lumineuses rouges sont observées séparées par des zones d’obscurité. on dit qu’elle est diffractée.
La figure de diffraction obtenue est formée de tâches lumineuses séparées de zones sombres.

Remarque: En remplaçant la fente par un obstacle très fin (un cheveu par exemple) on obtient les mêmes résultats que ceux trouvés précédemment.
2) Ia nature ondulatoire de la lumière
Le phénomène de diffraction montre que la lumière a un aspect ondulatoire. La lumière peut donc être caractérisée comme toutes les ondes, par sa célérité, sa fréquence et sa longueur d’onde.
II. propriété de l'onde lumineuse
1) La lumière monochromatique
La lumière monochromatique est une lumière qui ne se disperse pas quand elle travers un milieu dispersive.
Onde monochromatique
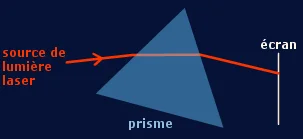
Une lumière monochromatique est caractérisée par sa couleur et sa fréquence qui sont indépendant du milieu traversé.
2) la célérité de la lumière
La vitesse de propagation de la lumière dépend du milieu de propagation, dans le vide la vitesse de propagation de la lumière est $C=3.10^8 \mathrm{~m} / \mathrm{s}$ et dans un milieu transparent, sa vitesse de propagation est $V=C / n \quad n$ est l’indice de réfraction du milieu
Remarque :
L’indice de réfraction $n=\frac{C}{V}=\frac{\lambda_0}{\lambda}>1$; $\lambda_0$ est la longueur d’onde dans le vide.
Remarque :
les longueurs d’onde des ondes électromagnétiques
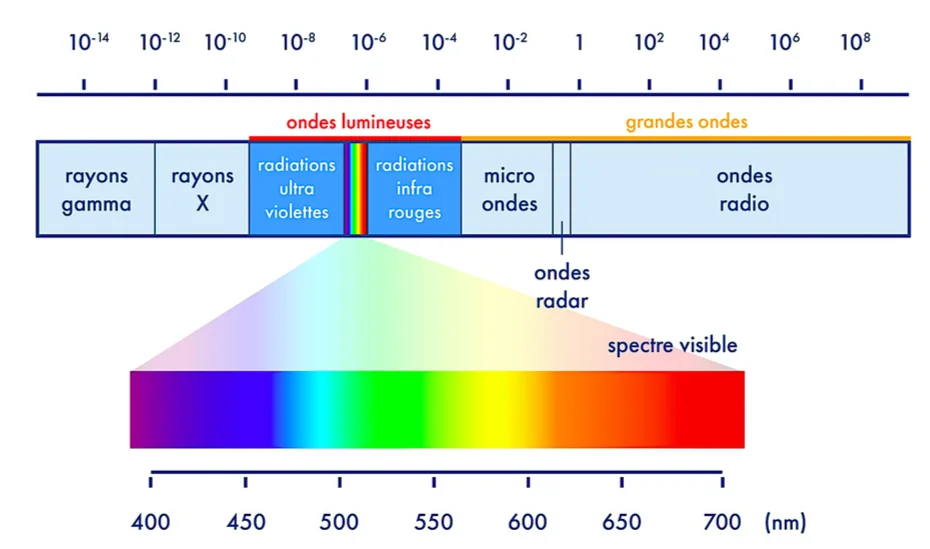
III. la diffraction de la lumière
1) étude experimental
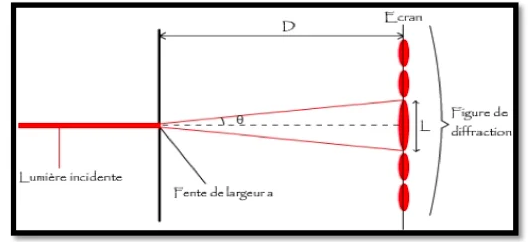
a) observation
La figure de diffraction observée est constituée de plusieurs taches:
* Une tache centrale plus grande et plus éclairée.
* Des taches latérales (plus petites et moins lumineuses), séparées par des zones d’extinction (zones sombres).
Ces taches s’étalent dans une direction perpendiculaire à celle de la fente.
Remarque
$>$ On obtient le même résultat si on remplace la fente par un fil mince.
$>$ Pour avoir une diffraction nette de la lumière il faut que $10 \lambda<a<100 \lambda$.
b) L’influence de la largeur de la fente
On utilise un laser de longueur d’onde $\lambda=650 \mathrm{~nm}$ on fait varier la valeur a de la largeur de la fente et on note les valeurs $L$ de la tache centrale observée sur un écran situé à une distance $D=1 \mathrm{~m}$ de la fente. on obtient
$$
\begin{array}{|c|c|c|c|}
\hline \text { a en } \mu \mathrm{m} & 40 & 50 & 100 \\
\hline \mathrm{~L} \text { en } \mathrm{cm} & 3,30 & 2,60 & 1,30 \\
\hline
\end{array}
$$
$$
\text { On remarque que la diffraction est d’autant plus nette que a est plus faible. }
$$
2) l’écart anqulaire $\theta$
On appelle écart angulaire $\theta$, l’angle, exprimé en radian, entre la droite passant par le milieu de la tache centrale et celle passant par le milieu de la première zone d’extinction. On a $\tan (\theta)=\frac{L}{2 . D}$ et $L \ll D$ donc $\theta$ et petit ce qui donne $\tan (\theta)=\theta$
$$
\theta=\frac{L}{2 . D}
$$
$$
\begin{array}{|c|c|c|c|}
\hline a(\mu \mathrm{~m}) & 40 & 50 & 100 \\
\hline 1 / \mathrm{a}\left(\mathrm{~m}^{-1}\right) & 25.10^3 & 20.10^3 & 10.10^3 \\
\hline \theta\left(10^{-3} \mathrm{rad}\right) & 16 & 13 & 6,5 \\
\hline
\end{array}
$$
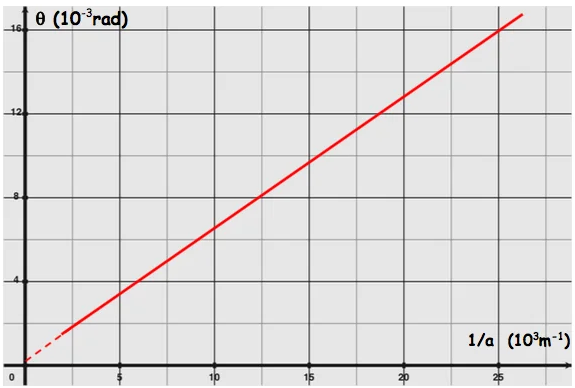
On constate que $\theta$ est proportionnel à $1 / a$ donc $\theta=k \cdot \frac{1}{a}$
$K$ facteur de proportionnalité on a $K=\frac{6,510^{-3}-0}{10.10^3-0}=6,50.10^{-6} \mathrm{~m}=\lambda$, donc $\theta=\lambda \cdot \frac{1}{a}$
Conclusion : on a : $\theta=\lambda \cdot \frac{1}{a}=\frac{L}{2 . D}$ donc $L=\frac{2 . \lambda . D}{a}=\frac{2 . C . D}{a \cdot v}$
Remarques:
✹la relation $L=\frac{2 \lambda D}{a}=\frac{2 \lambda_0 D}{a . n}$ est valable seulement pour une fente de largueur $a$ ou un obstacle d’épaisseur $a$.
✹ L’intensité de la lumière sur l’écran varie suivant la figure ci-dessous :
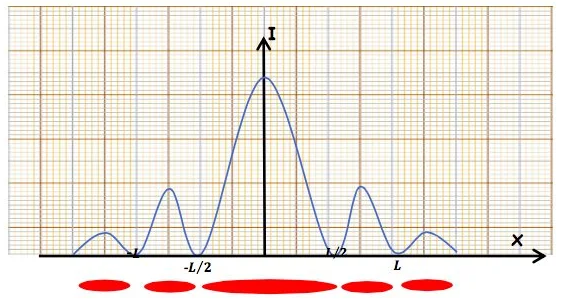
✹ la diffraction de la lumière blanche La figure de diffraction obtenue en utilisant la lumière blanche, présente une tache centrale blanche (superposition de toutes les lumières colorées visibles) de largeur égal à la tache violette et des taches latérales irisées
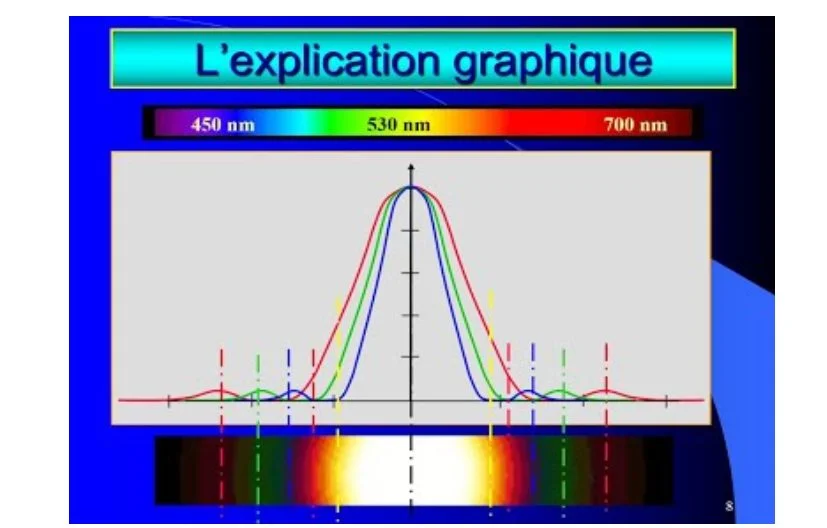
IV. La dispersion de la lumière.
1) Le prisme
Le prisme est un milieu transparent et homogène limité Par deux faces plans non parallèle formant un angle $A$

2) La réfraction de la lumière monochromatique.
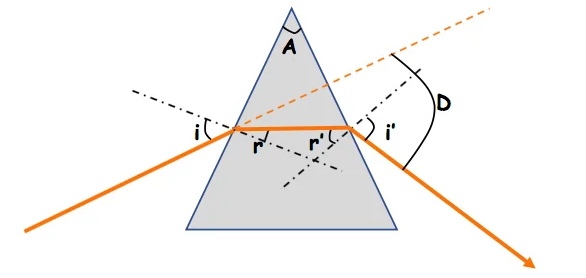
$$
\begin{array}{|c|c|}
\hline \sin (i)=n \cdot \sin (r) & \sin \left(i^{\prime}\right)=n \cdot \sin \left(r^{\prime}\right) \\
\hline A=r+r^{\prime} & D=i+i^{\prime}-A \\
\hline
\end{array}
$$
3) La dispersion de la lumière polychromatique

Le prisme est un milieu dispersif donc la vitesse de Propagation dépend de la fréquence (c.à.d de la couleur), et on a $V=C / n$, donc $n$ dépend de la couleur donc l’angle de déviation $D$ dépend de la couleur.
Remarque
✹ L’indice de réfraction $n$ dépend du milieu de propagation et de la couleur de la lumière : selon la relation $n=a+b / \lambda^2$
✹ $\lambda_R>\lambda_V$ donc $n_R<n_V$ ce qui donne $D_R<D_V$ donc le rouge est le moins dévié.
– Exercice 1
Répondre par Vrai ou Faux :
1- La célérité de la lumière est constante quel que soit le milieu de propagation, et vaut
$$
c=3.10^8 \mathrm{~m} / \mathrm{s}
$$
2- Les ondes lumineuses visibles dans le vide ont une longueur d’onde inférieur à 400 nm .
3- La fréquence d’une onde mécanique ou lumineuse dépend du milieu de propagation.
4- On réalise la diffraction d’une onde lumineuse par un obstacle :
4-1- La figure de diffraction obtenue par une fente de largeur ‘ $a$ ‘ est semblable à celle obtenue par un fil de diamètre ‘ $a$ ‘.
4-2- La direction de la figure de diffraction est perpendiculaire à la direction de la fente.
4-3- L’écart angulaire de la tache centrale ne dépend pas de la largeur de la fente.
4-4- Pour avoir la diffraction d’une lumière monochromatique il faut que cette lumière rencontre un obstacle ou une fente suffisamment grande.
4-5- L’indice de réfraction d’un milieu transparent dépend de l’onde lumineuse monochromatique se propageant dans ce milieu.
– Exercice 2
I-Un rayon laser traverse l’eau avec une célérité V. Les longueurs d’onde respectives de ce rayon dans le vide et dans l’eau sont $\lambda_0=632 \mathrm{~nm}$ et $\lambda=475,188 \mathrm{~nm}$.
On donne : la célérité de la lumière dans le vide $c=3.10^8 \mathrm{~m} / \mathrm{s}$.
1- Quelle la couleur correspondante à cette radiation.
2- Trouver la fréquence de cette radiation dans le vide et dans l’eau.
3- Trouver $n$ l’indice de réfraction de l’eau associé à cette radiation.
4- Déduire V.
II- L’indice de réfraction du verre est noté :
* $n_R$ pour la lumière rouge dont les longueurs d’onde respectives dans le vide et dans le verre sont $\lambda_{O R}=768 \mathrm{~nm}-\lambda_R=474,660 \mathrm{~nm}$
* $n_v$ pour la lumière violette dont les longueurs d’onde respectives dans le vide et dans le verre sont : $\lambda_{\mathrm{ov}}=434 \mathrm{~nm}-\lambda_v=262,712 \mathrm{~nm}$
1-Calculer $n_R$ et $n_V$. Conclure .
2- Calculer $v_R$ et $v_V$ les fréquences des deux radiations.
3- Calculer la célérité de chaque radiation dans le verre.